Bestäm samtliga heltalslösningar
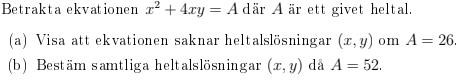
första ekvationen har ingen lösning för att vi har bara 1 faktor 2 och vi behöver 2 faktorer av samma tal för att kunna hitta en av variablerna. Jag vet dock inte hur jag ska uttrycka det matematiskt.
På andra ekvationen kom jag fram till att x = 2 och y = 6
sedan försökte jag faktorisera ekvationen ytterligare
men jag hittar inga fler lösningar för att 13 är ett primtal och man kan inte faktorisera det mer.
x(x+4y) ska kunna skrivas 1*52, 2*26, 4*13, 13*4, 26*2 eller 52*1. Skillnaden mellan faktorerna ska vara delbar med 4 så då är bara 2*26 och 26*2 kvar. 2*26 ger din lösning men x=26 och y=-6 är också en.
Och så har vi (-2)*(-26) och (-26)*(-2).
Laguna skrev:x(x+4y) ska kunna skrivas 1*52, 2*26, 4*13, 13*4, 26*2 eller 52*1. Skillnaden mellan faktorerna ska vara delbar med 4 så då är bara 2*26 och 26*2 kvar. 2*26 ger din lösning men x=26 och y=-6 är också en.
Och så har vi (-2)*(-26) och (-26)*(-2).
jag hänger inte riktigt med här, jag förstår lösningarna. Jag har löst ekvationerna och fått samma svar men det här med att faktorerna ska vara delbar med 4 ...
Skillnaden mellan faktorerna är x+4y - x = 4y. Det är delbart med 4.


