Bestäm sannolikheten att en slumpvis vald burk väger minst 395 g.
Företaget Konservburken tillverkar konservermed krossade tomater. På en viss sorts burkarmed krossade tomater anges att innehålletväger 400 gram. Som ett led i företagets kvali-tetskontroll vägs innehållet i ett antal burkar.Det visar sig att vikten är normalfördeladmed medelvikten 404 gram och standard-avvikelsen 5,0 gram. För att uppfylla företa-gets viktkrav ska burkarna innehålla minst395 gram krossade tomater. Bestäm sanno-likheten att en slumpvis vald konservburkinnehåller minst 395 gram krossade tomater.
Så vad jag gjorde var först få reda på täthetsfunktionen genom geogebra, vilket gav: 
Sedan körde jag integralen där p(0 till 394) för att få reda på sannolikheten att det ej blir minst 395. Alltså fick jag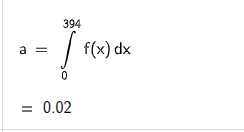
problemet här är att jag får 2 procent. Detta säger att det blir minst 395 är 98 procent. Men detta motsvarar ej facitet som står 96 procent . Vad har jag gjort för fel?
Du har frågan
Bestäm sanno-likheten att en slumpvis vald konservburkinnehåller minst 395 gram krossade tomater
vilket motsvarar
P[X≥395] = 1-P[X<395]=1-"din integral, men med 395 som övre integrationsgräns" = 0.96407
Märk väl att vikten är en kontinuerlig stokastisk variabel (om ni har pratat om det) så du kan inte "hoppa" i heltal ner till 394. Då missar du alla burkar i intervallet (394,395). Sedan är det inte så "noga" med < ≤ > ≥ när det är kontinuerliga s.v. utan även om det är logiskt att motsatsen till X≥395 är X<395 så har själva punkten x=395 "sannolikheten 0" och vi integrerar därmed upp t.o.m. 395. Vi kan alltså inte hålla på med en integrationsgränser som t.ex.
395-0.00000000000001
eller
395-0.00000000000000000000000000000000000001
etc. Det ger samma värde som 395 ändå, så att använda 395 gör inget för resultatet. Det är bra om du kan hålla strikt logik i uttryck som
P[X≥395] = 1-P[X<395]
men när det gäller övergången till integralberäkningen får man tänka "X≤395".
OBS! Detta gäller bara KONTINUERLIGA variabler. För DISKRETA är det mycket viktigt var gränserna går eftersom det (ofta) är heltal. Det är skillnad på att summera från 0 till 395 och 0 till 394.
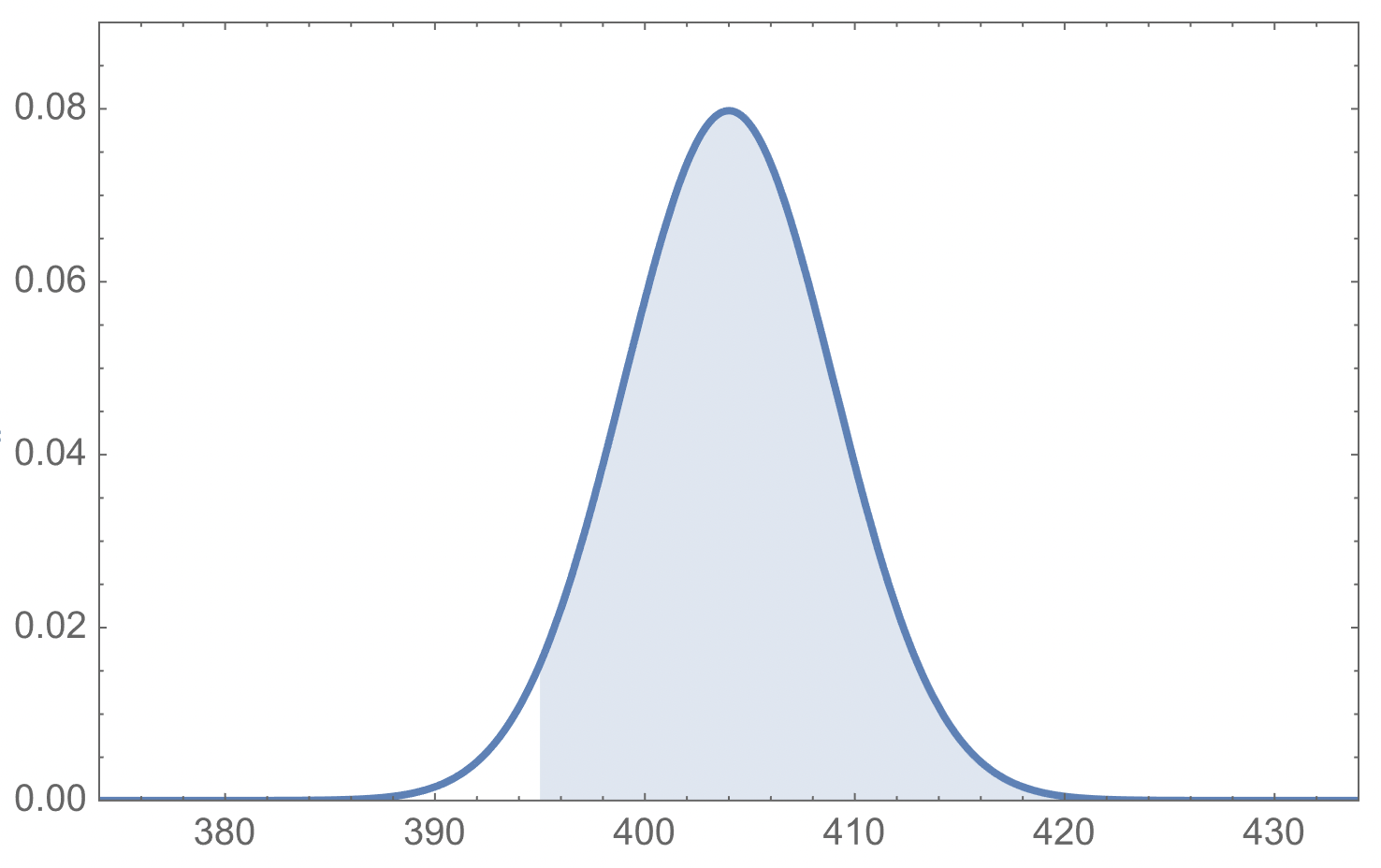
395 gram är 1.8 standardavvikelser under medeltiden.
Du söker phi(1.8) som man t.ex. hittar i någon tabell, 0.96407
EDIT: Egentligen 1 - phi(-1.8) som ju också är 0.96407

