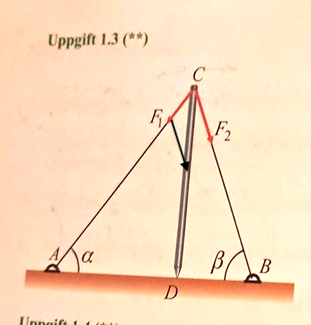
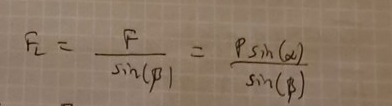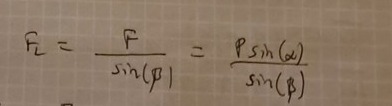Bestäm spännkraften i CB och kraftsummans storlek

Hej!
Jag försöker på alla möjliga sätt att hitta ett uttryck som liknar facit men kör fast och får inte som facit. Såhär gjorde jag!

destiny99 skrev:
Hej!
Jag försöker på alla möjliga sätt att hitta ett uttryck som liknar facit men kör fast och får inte som facit. Såhär gjorde jag!
Det stämmer alltså inte.
Använd att kraftsumman F är vertikal.
Pieter Kuiper skrev:destiny99 skrev:
Hej!
Jag försöker på alla möjliga sätt att hitta ett uttryck som liknar facit men kör fast och får inte som facit. Såhär gjorde jag!
Det stämmer alltså inte.
Använd att kraftsumman F är vertikal.
Vad menar de med att kraftsumman är vertikal om det inte är så att F=F1+F2?
destiny99 skrev:
Vad menar de med att kraftsumman är vertikal
Det innebär att summans horisontella komposant är noll.
Använd det.
Pieter Kuiper skrev:destiny99 skrev:
Vad menar de med att kraftsumman är vertikalDen innebär att summans horisontella komposant är noll.
Använd det.
Jag förstår inte riktigt. Var står det om horisontella komposant?
Pieter Kuiper skrev:destiny99 skrev:
Vad menar de med att kraftsumman är vertikalDet innebär att summans horisontella komposant är noll.
Använd det.
Jag får till slut detta. Men jag förstår inte varför de säger "kraftsumman F av de två spännkrafterna är F" för när man ska beräkna kraftsummans storlek så måste man använda F1y
och F2y.

destiny99 skrev:
jag förstår inte varför de säger "kraftsumman F av de två spännkrafterna är F"
Så står det inte i uppgiftens text.
Igen, det som var givet är att "kraftsumman F av de två spännkrafterna på masten i C är vertikal".
Pieter Kuiper skrev:destiny99 skrev:
jag förstår inte varför de säger "kraftsumman F av de två spännkrafterna är F"Så står det inte i uppgiftens text.
Igen, det som var givet är att "kraftsumman F av de två spännkrafterna på masten i C är vertikal".
Ja de menar alltså F1+F2=F? Formuleringen stör mig faktiskt eftersom de frågar om kraftsummans storlek
destiny99 skrev:
Ja de menar alltså F1+F2=F? Formuleringen stör mig faktiskt eftersom de frågar om kraftsummans storlek
Kraftsummans riktning var given, så det är endast storleken som behöver bestämmas.
Pieter Kuiper skrev:destiny99 skrev:
Ja de menar alltså F1+F2=F? Formuleringen stör mig faktiskt eftersom de frågar om kraftsummans storlekKraftsummans riktning var given, så det är endast storleken som behöver bestämmas.
Aa jo det stämmer att de söker storleken på kraftsumman F. Men varför är det y-komposanterna till F1 och till F2 som ger den storleken och inte vanligt uttryck för F1 och F2 som kan göra det?
F1 och F2 är, precis som alla andra krafter, vektorer och måste behandlas som sådana när du utför beräkningar. F är alltså summan av vektorerna F1 och F2.
Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0.
Ture skrev:F1 och F2 är, precis som alla andra krafter, vektorer och måste behandlas som sådana när du utför beräkningar. F är alltså summan av vektorerna F1 och F2.
Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0.
Du menar att F1y+F2y=0 samt F1x+F2x=0?
destiny99 skrev:Ture skrev:F1 och F2 är, precis som alla andra krafter, vektorer och måste behandlas som sådana när du utför beräkningar. F är alltså summan av vektorerna F1 och F2.
Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0.Du menar att F1y+F2y=0 samt F1x+F2x=0?
inte riktigt,
F1y+F2y= F
samt
F1x+F2x=0
Ture skrev:destiny99 skrev:Ture skrev:F1 och F2 är, precis som alla andra krafter, vektorer och måste behandlas som sådana när du utför beräkningar. F är alltså summan av vektorerna F1 och F2.
Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0.Du menar att F1y+F2y=0 samt F1x+F2x=0?
inte riktigt,
F1y+F2y= F
samt
F1x+F2x=0
Men varför är F1y+F2y=F ? Du nämnde att summan av F1 och F2 :s komposanter i alla riktningar är 0?
Nej, jag skrev i alla andra riktningar än nedåt
Ture skrev:Nej, jag skrev i alla andra riktningar än nedåt
Det förstår jag inte. Nedåt och lika med 0?
"Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0."
Detta är vad du skrev Ture.
Nu har jag markerat i fetstil
"Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0."
Ture skrev:Nu har jag markerat i fetstil
"Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0."
Hur är komposanterna i alla andra riktningar 0? Jag skrev tidigare F1y=F2y men det höll du inte med , däremot sade du att F1x =F2x är sant , Vad är det du menar annars med ditt feta stil?
destiny99 skrev:Ture skrev:Nu har jag markerat i fetstil
"Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0."
Hur är komposanterna i alla andra riktningar 0?
Summan i alla horisontella riktningar är noll.
Det är bara att rita: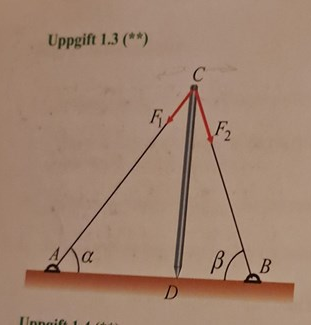 I en formel: , dessa två komposanter är lika stora.
I en formel: , dessa två komposanter är lika stora.
Alltså: .
Pieter Kuiper skrev:destiny99 skrev:Ture skrev:Nu har jag markerat i fetstil
"Om summan av F1 och F2 är riktad nedåt, måste summan av F1 och F2s komposanter i alla andra riktningar vara = 0."
Hur är komposanterna i alla andra riktningar 0?
Summan i alla horisontella riktningar är noll.
Det är bara att rita:I en formel: , dessa två komposanter är lika stora.
Alltså: .
Jo jag fick samma som dig , men hur kommer det sig att F1y+F2y inte är lika med 0? Är det pga deras riktningar är vertikala och kraftsummans riktning är vertikal?
destiny99 skrev:men hur kommer det sig att F1y+F2y inte är lika med 0?
Kolla ritningen!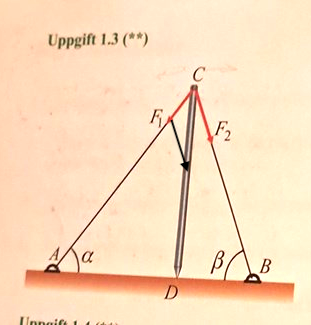
Pieter Kuiper skrev:destiny99 skrev:men hur kommer det sig att F1y+F2y inte är lika med 0?
Kolla ritningen!
Jahaaa du har parallellförflyttat F2 där spetspen på F1 och om man resulterande linje från C till spetsen på den svarta pilen så har vi F kraftsumman.