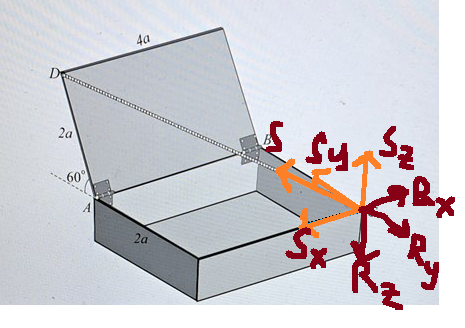
Bestäm spännkraften S i repet då luckan bildar vinkeln 60 med horisontalen
Har du provat att ställe upp någon sorts ekvation? Du skulle t.ex kunna utnyttja att luckan är i vila (newtons första lag F_R = 0).
Lasse Vegas skrev:Har du provat att ställe upp någon sorts ekvation? Du skulle t.ex kunna utnyttja att luckan är i vila (newtons första lag F_R = 0).
Nej det har jag inte för jag är osäker på om alla dessa uppställda krafter räcker. Ja jag kan absolut ställa upp kraftjämvikt. Men tänker på den där vinkeln 60 grader , kan man få in i den i spännkraft trigonometri på något sätt?
Vad är Rx och Ry för krafter?
Lasse Vegas skrev:Vad är Rx och Ry för krafter?
Reaktionskrafter
Okej, tänk också på att det spännkraften S lär ha en komponent i z-led eftersom vi kollar i ett 3d-koordinatsystem.
Lasse Vegas skrev:Okej, tänk också på att det spännkraften S lär ha en komponent i z-led eftersom vi kollar i ett 3d-koordinatsystem.
Hm jag ser inte hur det är i 3d tyvärr. Jag trodde allt var i 2D.
Lådan är ett föremål i 3d. I 3d har vi tre olika riktningar, då är det rimligt att det finns en komposant för varje riktning. Så det borde se något i den här stilen.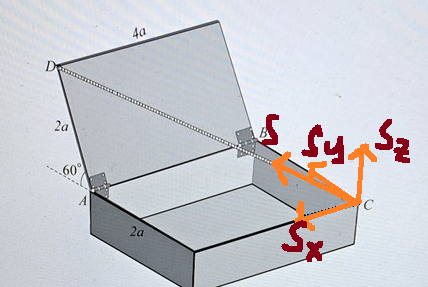
Krafterna är inte ritade till skala.
Lasse Vegas skrev:Lådan är ett föremål i 3d. I 3d har vi tre olika riktningar, då är det rimligt att det finns en komposant för varje riktning. Så det borde se något i den här stilen.
Krafterna är inte ritade till skala.
Jaha okej men Sz kommer vara där reaktionskrafterna ligger . Ska man flytta reaktionskrafterna?
Aa nästan. Spännkraftena kommer se ut på sättet jag skickade i bilden ovan. Reaktionskrafterna kommer då att ha motsatt riktning, så i din bild ser R_x rätt ut men R_y borde egentligen vara riktad motsatt S_y. Om S_z pekar upp från marken så skulle reaktionskraften R_z peka neråt mot marken på det här sättet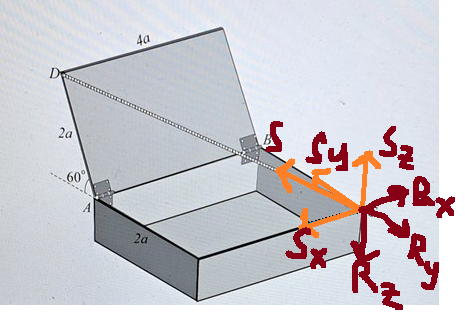
Lasse Vegas skrev:Aa nästan. Spännkraftena kommer se ut på sättet jag skickade i bilden ovan. Reaktionskrafterna kommer då att ha motsatt riktning, så i din bild ser R_x rätt ut men R_y borde egentligen vara riktad motsatt S_y. Om S_z pekar upp från marken så skulle reaktionskraften R_z peka neråt mot marken på det här sättet
Jaha okej
Jag tror dock inte att reaktionskrafterna är nödvändiga för att lösa uppgiften. Jag försöker lösa uppgiften just nu men har fastnat på lite trig. i 3d. Har inte hållt på med det allt för mycket.
Lasse Vegas skrev:Jag tror dock inte att reaktionskrafterna är nödvändiga för att lösa uppgiften. Jag försöker lösa uppgiften just nu men har fastnat på lite trig. i 3d. Har inte hållt på med det allt för mycket.
Okej men jag är också fast och vet inte justnu var jag ska börja 😅 ritade ut alla krafter vi pratade om
En av de första sakerna som jag tänkte att man kunde göra är att ställa upp momentjämvikt för luckan kring O.
Lasse Vegas skrev:En av de första sakerna som jag tänkte att man kunde göra är att ställa upp momentjämvikt för luckan kring O.
Hm jag ser inget O? Här är mina kraftjämvikt
Oj, förlåt, jag är så van vid att man kallar rotationsaxeln för O. Jag syftar på axeln AB som luckan sitter fast i.
Lasse Vegas skrev:Oj, förlåt, jag är så van vid att man kallar rotationsaxeln för O. Jag syftar på axeln AB som luckan sitter fast i.
Detta ger dock inte rätt svar för S
Är det möjligt att kanske räkna på vektorn DC och sen multiplicera med kraften S på vekorform? Isåfall behöver vi koordinaterna för D och C. Hur kan man ta reda på koordinaterna för D och C?
För att räkna med vektorer behöver man införa ett koordinatsystem. Så man får välja en punkt som origo och sedan bestämma andra vektorer genom sträckor i bilden.
Lasse Vegas skrev:För att räkna med vektorer behöver man införa ett koordinatsystem. Så man får välja en punkt som origo och sedan bestämma andra vektorer genom sträckor i bilden.
Ja detta är vad jag har nu. Så hur gör vi? Målet är att räkna ut vektorn DC. Min spontana tanke är att Dx=a*sqrt(3)
Jag vet inte riktigt om det här kommer fungera, är egentligen inte supervan med statik i 3d men jag ska försöka hjälpa till där det går. För att hitta vektorn DC behöver du först hitta vektorerna C och D. Att hitta vektorerna C och D är samma sak som att bestämma deras koordinater. Vektorn C har till exempel koordinaterna (4a, 2a, 0).
Lasse Vegas skrev:Jag vet inte riktigt om det här kommer fungera, är egentligen inte supervan med statik i 3d men jag ska försöka hjälpa till där det går. För att hitta vektorn DC behöver du först hitta vektorerna C och D. Att hitta vektorerna C och D är samma sak som att bestämma deras koordinater. Vektorn C har till exempel koordinaterna (4a, 2a, 0).
Ja precis jag håller med. C har koordinaterna (4a,2a,0) och hur kan man ta reda på koordinaterna för D?
Du kan tänka: hur måste jag röra mig längs axlarna för att komma till D? Ett sätt att göra det på är så här:
Lasse Vegas skrev:Du kan tänka: hur måste jag röra mig längs axlarna för att komma till D? Ett sätt att göra det på är så här:
Okej men det ser ut som en likbent triangel med vinklarna 60,60 och 120? Jag vet dock inte hur man kan bestämma koordinaterna för D när det ser ut sådär. Jag tänkte mer om vi hade en rätvinklig triangel.
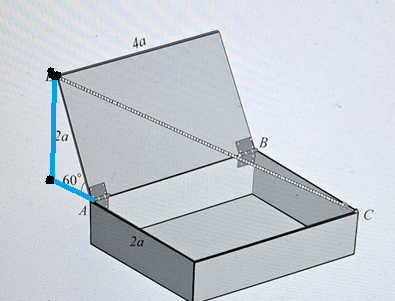
Aa den är lite missvisande i figuren. Tanken är i alla fall att du måste bestämma storleken på de blå vektorerna för att få koordinaterna för D. Så här ser det ut i ursprungliga bilden
Här ser man tydligt att sträckorna utgör basen och höjden i en triangel och kan bestämmas mha trig.
Lasse Vegas skrev:Aa den är lite missvisande i figuren. Tanken är i alla fall att du måste bestämma storleken på de blå vektorerna för att få koordinaterna för D. Så här ser det ut i ursprungliga bilden
Jaha okej då får jag kanske jag rita DA typ lite lutande som i uppgiften. Då får vi en rätvinklig triangel då med x=2acos60 samt y=2asin60
Ja, du har rätt mått på sidorna men själva koordinaterna kommer skilja lite.
Lasse Vegas skrev:Ja, du har rätt mått på sidorna men själva koordinaterna kommer skilja lite.
Juste sorry. Vi kommer få y=-2acos60 och z=2asin60 för D
Nästan helt rätt. Det ska fortfarande vara cos(60) för y-koordinaten.
Lasse Vegas skrev:Nästan helt rätt. Det ska fortfarande vara cos(60) för y-koordinaten.
Ja precis! Då kan man räkna ut vektorn DC som (4a,2a,0)-(0,-2acos60,2asin60)=(4a,3a,-asqrt(3))
Sen vill vi räkna ut momentet map på AB eftersom vi har S på vektorform men vi vet inte dess belopp. Då är det bara mg och S som verkar? Vilka momentarmar har de då?
Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Men spännkraftens hävarm är väl längden AB . Tyngdkraften har ju mg(0,0,-1) men dess hävarm blir väl AB/2?
Hävarmen borde på något sätt gå från axeln till punkten där kraften appliceras. Men det verkar fungera annorlunda om man ska bestämma momentet kring en axel i 3d. Sååå här tar det nog stop för mig faktiskt. Hoppas det löser sig!
Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Det här gäller nog alltså inte. Vi får vänta tills det kommer någon mer kunnig och hjälper.
Lasse Vegas skrev:Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Det här gäller nog alltså inte. Vi får vänta tills det kommer någon mer kunnig och hjälper.
Det finns ju annars att man kan beräkna momentet som M=rab×F
Omkring 7:00 i det här klippet så kör dem ett exempel där de bestämmer momentet kring en axel.
Engineering Mechanics: Statics Theory | Calculating Moments in 3D about a Point or Axis
destiny99 skrev:Lasse Vegas skrev:Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Det här gäller nog alltså inte. Vi får vänta tills det kommer någon mer kunnig och hjälper.
Det finns ju annars att man kan beräkna momentet som M=rab×F
Det var det jag trodde planen var just nu, att på något sätt komma fram till det. Att bestämma momentarmen och kryssa det med kraftvektorn på något sätt och få en ekvation.
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Det här gäller nog alltså inte. Vi får vänta tills det kommer någon mer kunnig och hjälper.
Det finns ju annars att man kan beräkna momentet som M=rab×F
Det var det jag trodde planen var just nu, att på något sätt komma fram till det. Att bestämma momentarmen och kryssa det med kraftvektorn på något sätt och få en ekvation.
Yes men vi vet att r_AB=(1,0,0) eftersom A=(4a, 2a,0). Känns som att A och B har samma koordinaterna?
Lasse Vegas skrev:destiny99 skrev:Lasse Vegas skrev:Lasse Vegas skrev:Bör vara där krafterna verkar. Då gäller det att plocka fram nya koordinater där det behövs. Spännkraften verkar i punkten D, vilket du redan kan koordinaterna för. Tyngdkraften verkar i mitten av locket eftersom den är homogen och då måste vi bestämma de koordinaterna.
Det här gäller nog alltså inte. Vi får vänta tills det kommer någon mer kunnig och hjälper.
Det finns ju annars att man kan beräkna momentet som M=rab×F
Det var det jag trodde planen var just nu, att på något sätt komma fram till det. Att bestämma momentarmen och kryssa det med kraftvektorn på något sätt och få en ekvation.
Om man istället fokuserar på momentet kring A så kan man väl räkna ut r_ad×S+r_ag×Mg=0? Vi behöver dock veta koordinaterna för masscentrum av lockets massa dvs rg samt A:s koordinater
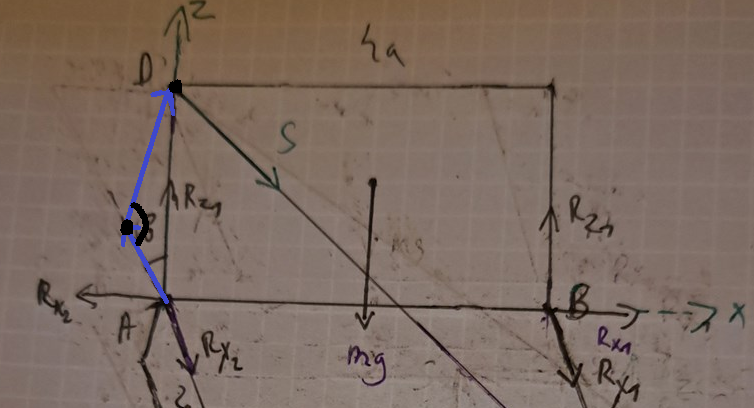
Ett försök med annat koordinatsystem.
Jan Ragnar skrev:Ett försök med annat koordinatsystem.
Hur kan jag bestämma koordinater för G ?
Vilken punkt är G?
Jan Ragnar skrev:Vilken punkt är G?
Masscentrum för G som verkar där mg verkar om vi antar att luckan är homogen. Jag vill ju använda momentpunkten i A för att beräkna MA=rAD×S+rAG×Mg om vi antar A är origo. Jag vet ju AD ,men mitt problem är hur jag ska ta fram koordinaterna för G..
I det koordinatsystem jag skissat så har lockets mittpunkt koordinaterna (a,2a,0), men jag tror inte det är så betydelsefullt. Krafterna Sx och Sy tas upp av gångjärnskonstruktionen. När man tittar på momentet från locket så är det enbart Sz som balanserar det.
Jan Ragnar skrev:I det koordinatsystem jag skissat så har lockets mittpunkt koordinaterna (a,2a,0), men jag tror inte det är så betydelsefullt. Krafterna Sx och Sy tas upp av gångjärnskonstruktionen. När man tittar på momentet från locket så är det enbart Sz som balanserar det.
Men jag ser inte hur du använder dig av M_A=r_AD×S+r_AG×Mg vilket är det jag är ute efter
Nej jag använder inte det, så tyvärr kan jag inte stå till hjälp med ditt önskemål.
Jag glömde fråga dig om du har facit till uppgiften.
Jan Ragnar skrev:Nej jag använder inte det, så tyvärr kan jag inte stå till hjälp med ditt önskemål.
Jag glömde fråga dig om du har facit till uppgiften.
Facit säger 1/2*sqrt(7/3)*mg. Men såhär får jag . Det blir fortfarande inte rätt.
