Bestäm storleken på området Emil kan röra sig i.
Emil och hans lillasyster ska leka tafatt ('kull' på stockholmska) och det bestäms att Emil skall vara jagare. För att göra det rättvist beslutas att Emil ska bindas fast med en tjugo meter lång lina mot ett cylinderformat skjul som finns på gården. Hur stor area kan Emil röra sig på om skjulet har diametern 20 meter?
Här har vi en bild för att förtydliga lite grann:

Kallaskull skrev:
Nja, det är tyvärr fel. Hur kommer du fram till det?
Jag tänkte inte på att linan kan böja på sig i första, är det
Förra gången jag såg den här trodde jag att det inte fanns någon sluten lösning, men nu var det lätt, så jag har säkert gjort fel. Kan svaret vara 200 pi + 800/3?
m^2.
Laguna skrev:Förra gången jag såg den här trodde jag att det inte fanns någon sluten lösning, men nu var det lätt, så jag har säkert gjort fel. Kan svaret vara 200 pi + 800/3?
m^2.
200pi kommer från halvcirkeln men var ifrån kommer 800/3 ifrån?
Om skjulets vägg är rak istället för krökt, så sveper Emil ut en halvcirkel med den konstanta radien 20 meter. När skjulets vägg är krökt kommer Emil att svepa ut ett område vars ''radie'' ändras beroende på var han befinner sig.
Laguna skrev:Förra gången jag såg den här trodde jag att det inte fanns någon sluten lösning, men nu var det lätt, så jag har säkert gjort fel. Kan svaret vara 200 pi + 800/3?
m^2.
Det är tyvärr också fel.
Det skulle hjälpa mig att styra in er på rätt banor om ni säger hur ni tänker! Jag förstår att är en halvcirkel, men vad är ?
Som Albiki nämner är det viktigt att ha i åtanke att linan kröker sig runt skjulet vilket gör att "cirkelns radie" blir kortare och kortare.
Har med numeriska metoder kommit fram till 200pi+682.713. Lyckas inte integrera integralen med polära koordinater för hand.
Om man sätter upp en dubbelintegral för arean, gör ngn variabelbyte och gränserna blir: Radien (repets längd ändring) går från 20->0 och vinkeln 0->pi? Dock vet jag inte hur ev funktion skulle se ut. Hmm
parveln skrev:Har med numeriska metoder kommit fram till 200pi+682.713. Lyckas inte integrera integralen med polära koordinater för hand.
Nja, det där blev orimligt stort (större än om Emil får röra sig fritt i en hel cirkel med radie ). Vad ställer du upp för integraler?
Ställer upp integralen för arean av arean på höger sida och subtraherar med cirkelsegmentets area (100-50(sin2))
Insåg att jag glömde dela med 2 och nu får jag istället arean 200pi+260.149
Integralen är följande: https://www.wolframalpha.com/input/?i=integrate+(((200-200*cos(2v))%5E1%2F2-20v%2B20)%5E2%2F2)+from+0+to+1
(Återkommer med bild)
parveln skrev:Ställer upp integralen för arean av arean på höger sida och subtraherar med cirkelsegmentets area (100-50(sin2))
Insåg att jag glömde dela med 2 och nu får jag istället arean 200pi+260.149
Integralen är följande: https://www.wolframalpha.com/input/?i=integrate+(((200-200*cos(2v))%5E1%2F2-20v%2B20)%5E2%2F2)+from+0+to+1
(Återkommer med bild)
Det är väldigt nära. Jag får närmevärdet till vilket skiljer sig på någon decimal mot ditt svar. Antagligen är det samma svar med ett avrundningsfel i antingen dina eller mina beräkningar.
Dessvärre begriper jag inte hur du kommit fram till ditt svar. Vad beräknas med den där integralen? Hur kommer du fram till med hjälp av den?
Jag prova rita en(icke skalenlig) bild av hur den ungefär kommer se ut, jag satte en cirkel med radie r med mittpunkt i origo och cirkel sektor längden från x-axeln till vinkeln v plus längden upp till funktionen kommer vara konstant. Jag vet inte riktigt vilken vinkel linjen vid cirkelns periferi ska ha för att vara korrekt eller hur man kan sätta upp en funktion där funktionen som beror på v vilket i sig beror på x, kan man på något sätt använda detta för att lösa problemet?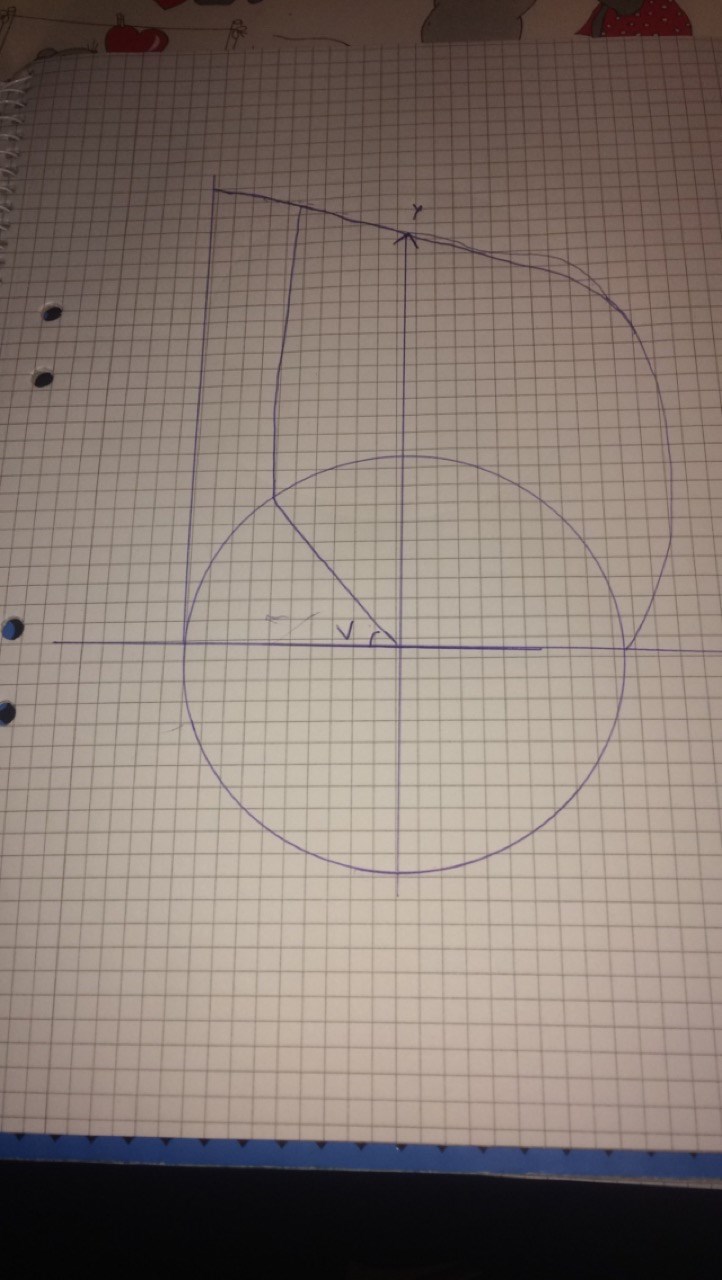
Jag hänger inte helt med på vad din bild beskriver. Jag kanske kan bidra med en bild på hur området kommer att se ut:
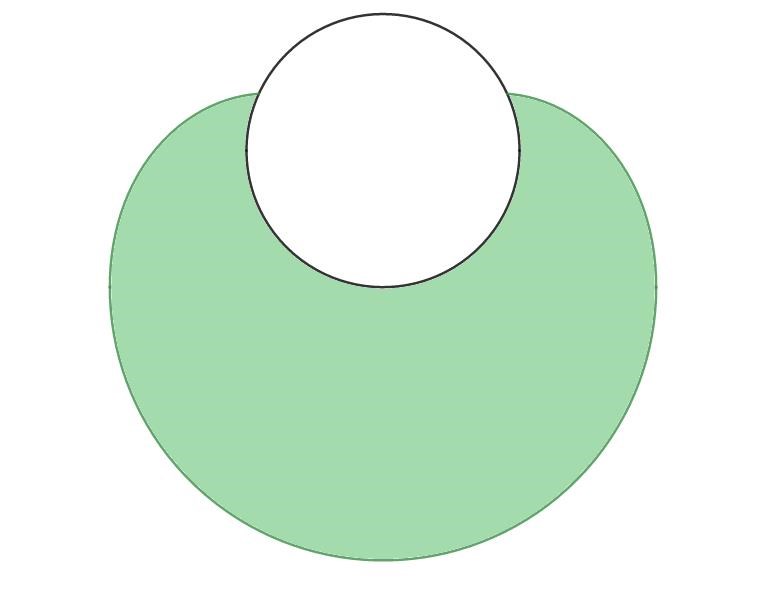
AlvinB skrev:parveln skrev:Ställer upp integralen för arean av arean på höger sida och subtraherar med cirkelsegmentets area (100-50(sin2))
Insåg att jag glömde dela med 2 och nu får jag istället arean 200pi+260.149
Integralen är följande: https://www.wolframalpha.com/input/?i=integrate+(((200-200*cos(2v))%5E1%2F2-20v%2B20)%5E2%2F2)+from+0+to+1
(Återkommer med bild)
Det är väldigt nära. Jag får närmevärdet till vilket skiljer sig på någon decimal mot ditt svar. Antagligen är det samma svar med ett avrundningsfel i antingen dina eller mina beräkningar.
Dessvärre begriper jag inte hur du kommit fram till ditt svar. Vad beräknas med den där integralen? Hur kommer du fram till med hjälp av den?
Vad bra att det blir liknande svar, då är jag kanske inte helt ute och cyklar. Jag börjar med att tänka mig att väggen inte existerar och att Emil rör sig med en lina med längden r som dock ändras hela tiden. Linans egentliga längd är 20m. I varje tidpunkt kan en del av linan tänkas vara virad runt cirkeln och en del vara "fri". Den fria delen kan beräknas genom att ta 20-(delen som är virad). Delen som är virad är helt enkelt längden av den cirkelsektor som repet är virat runt, dvs v*r, där v är mittpunktsvinkeln i radianer och r=10 är radien.
Nu skulle vi dock tänka på repet som att det gick genom cirkeln, vilket innebär att vi tänker att repets längd är den fria längden+det kortaste avståndet mellan cirkelns botten(där Emil är fastknuten) och punkten där repet slutar ligga mot cirkelns kant. Denna kan beräknas med hjälp av cosinussatsen till där l är det kortaste avståndet mellan punkterna och v mittpunktsvinkeln. För att kunna ställe upp en vettig integral vill vi dock inte arbeta med mittpunktsvinkeln utan istället med vinkeln som heter v' i min bild som bifogas nedan. Med hjälp av lite geometri kan vi uttrycka v som 2*v'. Att finna arean blir nu helt enkelt att ställa upp en integral för beräkning av arean med polära koordinater enligt http://tutorial.math.lamar.edu/Classes/CalcII/PolarArea.aspx vår funktion som ska integreras är r(v')=. Arean som beräknas kommer dock att vara för stor eftersom vi räknar med som går genom cirkeln, dvs arean av ett cirkelsegment med mittpuntksvinkeln 2 radianer. Denna har arean 100-50sin(2rad). Arean blir alltså totalt 200pi+((integralens värde)-100+50sin2)*2, multiplicerat med två eftersom Emil kan springa åt vänster och inte bara hörnet, det blir ingen dubbelräkning eftersom mittpunktsvinkeln är 2 radianer vilket är mindre än pi radianer.
Jag tänkte att ifall vi tar bort den undre halvcirkeln och vänder på figuren 90 grader medurs och sätter cirkelns medelpunkt i origo med radie r kanske vi kan hitta någon funktion som beskriver "funktionen" vilket jag kallar repets bana.
Här är en bild på min figur
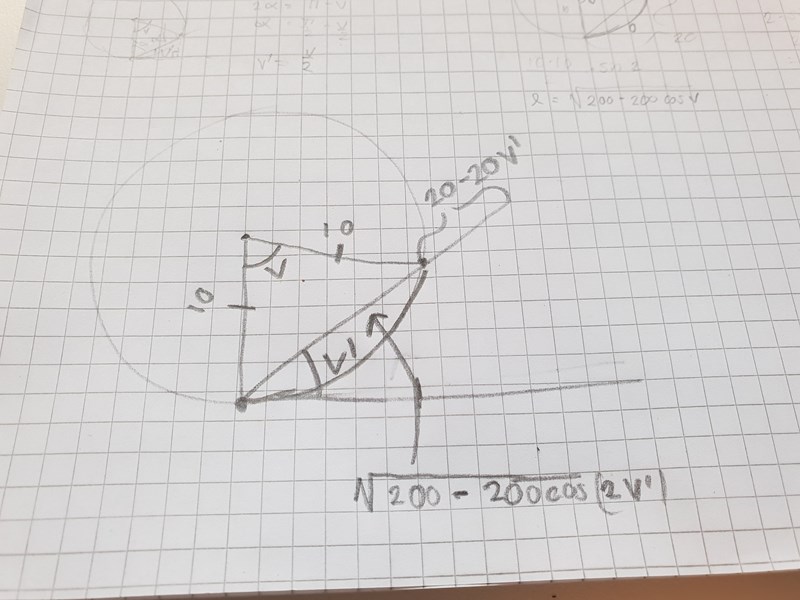
parveln skrev:Här är en bild på min figur
[...]
Smart! Att räkna med polära koordinater och sedan dra bort biten av cirkeln man då räknar med hade jag inte tänkt på. Själv delade jag upp i flera integraler med parametriseringar vilket ledde till långa beräkningar.
Något som kan hjälpa när du ska beräkna integralen exakt är att i intervallet du integrerar över. När man väl gjort den förenklingen får man en hyfsat dräglig integral som kan lösas med standardknepen.
AlvinB skrev:parveln skrev:Här är en bild på min figur
[...]
Smart! Att räkna med polära koordinater och sedan dra bort biten av cirkeln man då räknar med hade jag inte tänkt på. Själv delade jag upp i flera integraler med parametriseringar vilket ledde till långa beräkningar.
Något som kan hjälpa när du ska beräkna integralen exakt är att i intervallet du integrerar över. När man väl gjort den förenklingen får man en hyfsat dräglig integral som kan lösas med standardknepen.
Ja! Såklart att det blir det. Får ta och räkna på det lite senare idag
Hur går det? Jag kan ju absolut göra fel, men nu har jag provat två olika metoder och räknat ut dem numeriskt och fått samma svar båda gångerna för det som är utanför halvcirkeln, nämligen 800/3.
Laguna skrev:Hur går det? Jag kan ju absolut göra fel, men nu har jag provat två olika metoder och räknat ut dem numeriskt och fått samma svar båda gångerna för det som är utanför halvcirkeln, nämligen 800/3.
Ja, jag kan ju bara säga att det så vitt jag vet inte är rätt svar. Jag får nämligen arean exklusive halvcirkeln till ca. areaenheter.
Det är möjligt att jag gör någon tankevurpa, men det är omöjligt att säga om du inte visar din uträkning.
Jag låter radien vara 1 i stället, så kan man multiplicera allt med 100 efteråt.
Repet har längden 2, och jag låter l vara den längd som ligger an mot cylindern. Därmed är vinkeln på den cirkelsektorn också l (radianer).
Min ena metod betraktar den fria raka delen av repet och låter den svepa upp en area som består av liksidiga (i limes) trianglar med en vinkel dl och långa sidorna = 2-l. Ytan är integralen av 1/2*(2-l)^2 från 0 till 2 = 4/3.
Min andra metod har jag inte beräknat något slutet uttryck för. Jag delar upp ytan i horisontella strimlor. Jag itererar över l, som går från 0 till 2 med steg dl (något lämpligt valt, t.ex. 1/100000). För varje värde på l beräknar jag var Emil är (x2, y2) och tar sedan reda på punkten på cylindern med samma y, med x = x1. Höjden på strimlan är y2(l+dl) - y2(l), och jag adderar alla strimlor. Högst upp händer det intressanta att det finns flera värden på l med samma y2, men det blir rätt i alla fall, för att man beräknar en för stor strimla på vägen upp till maximala y2, och sedan drar bort det som var för mycket, genom att dy blir negativ.
Numeriskt får jag som sagt också värden som ligger nära 4/3. 1.3333 i alla fall i det senare fallet.
Jag måste erkänna att jag gjort fel. :-)
Laguna har tagit fram rätt svar. Felet som jag och parveln gör är att vi tänker att det längsta man kan komma från cirkeln i varje punkt på den är om man fortsätter i samma riktning som från origo till punkten:

Men så är inte fallet. Det längsta man kommer i varje punkt på cirkeln är nämligen om man fortsätter i samma riktning som cirkelns tangent. Det ger en lite större area:

Man kan sedan skapa en parametrisering utifrån detta:
där är vinkeln (mätt i radianer) i cirkeln som representerar skjulet. Med hjälp av detta kan man ställa upp en integral och få att:
Hatten av till Laguna för en mycket kort och koncis lösning med sin första metod. Jag får kanske ta och studera problemen lite grundligare innan jag dömer vad som är rätt och fel i framtiden. :-)
Tack!






