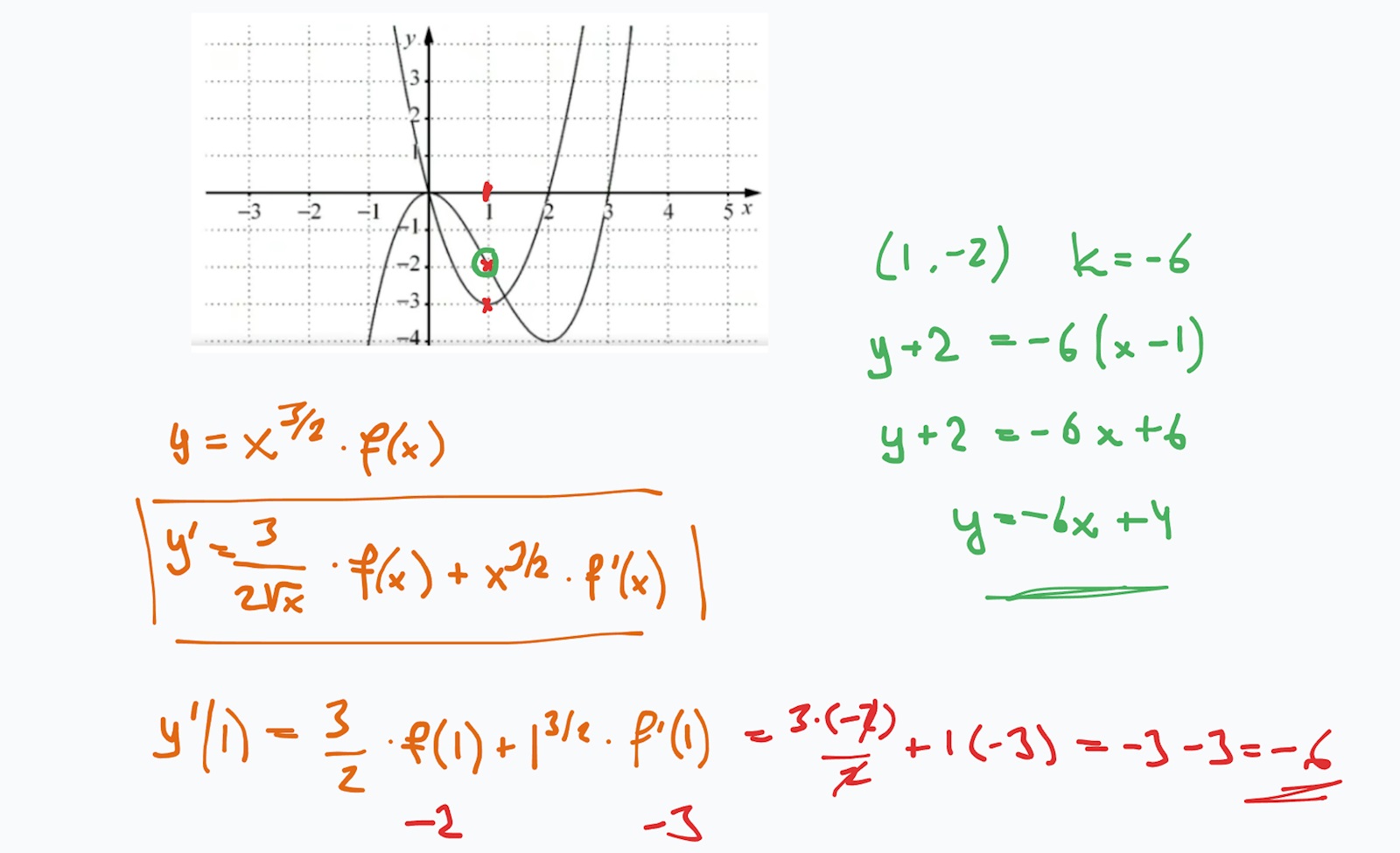jag vet ju att tangenten dvs
Ja, det stämmer.
Sätt och ta med hjälp av produktregeln fram ett uttryck för .
Du kan då med hjälp av de givna graferna bestämma tangentens lutning .
Kommer du vidare då?
Yngve skrev:Ja, det stämmer.
Sätt och ta med hjälp av produktregeln fram ett uttryck för .
Du kan då med hjälp av de givna graferna bestämma tangentens lutning .
Kommer du vidare då?
jag kan väl använda produktregeln ?
Om det är meningen att man skall beräkna (gissa) vad f(x) är så skulle jag ansätta
f(x)=Ax^2(x-3)+B
med f(0)=0 vilket ger B=0 och f(2)=-4 vilket ger A=1.
Trinity2 skrev:Om det är meningen att man skall beräkna (gissa) vad f(x) är så skulle jag ansätta
[...]
Jag tror inte att det är meningen.
Arup skrev:
jag kan väl använda produktregeln ?
Ja, gör det och visa vad du kommer fram till.
När du väl har beräknat k-vördet så kan du bestämma m i tangentens ekvation y = kx+m genom att använda en känd punkt på grafen till y = f(x).
Fick lite tips från livehjälpen.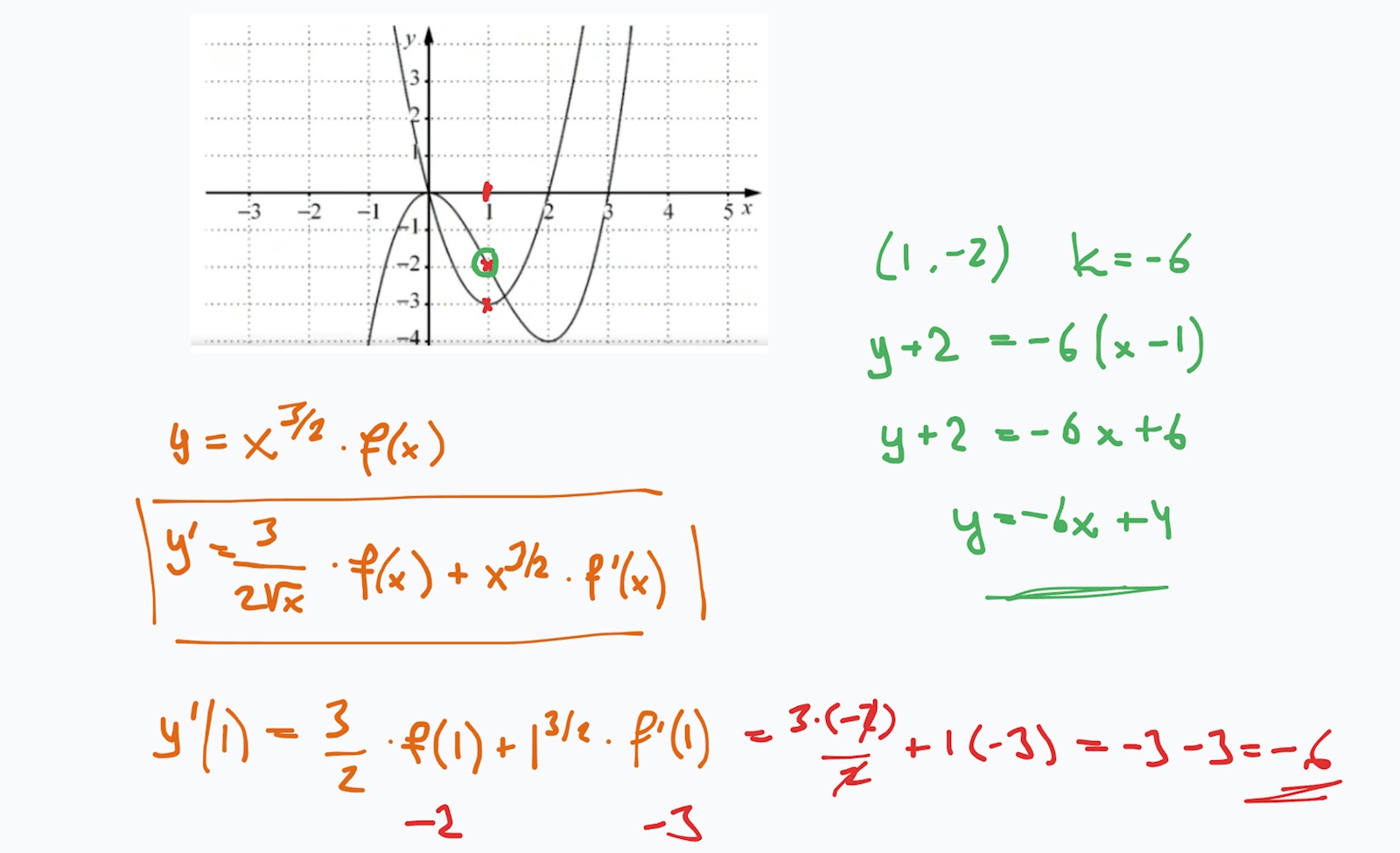
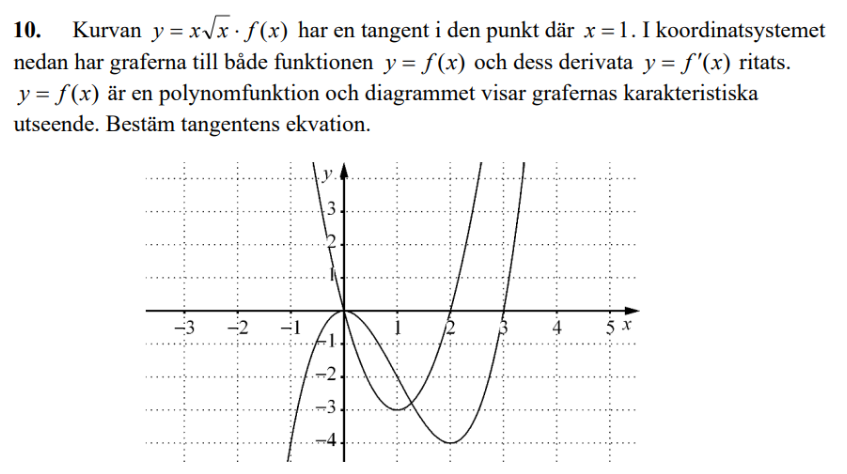
Så här ser funktionen och dess derivata ut
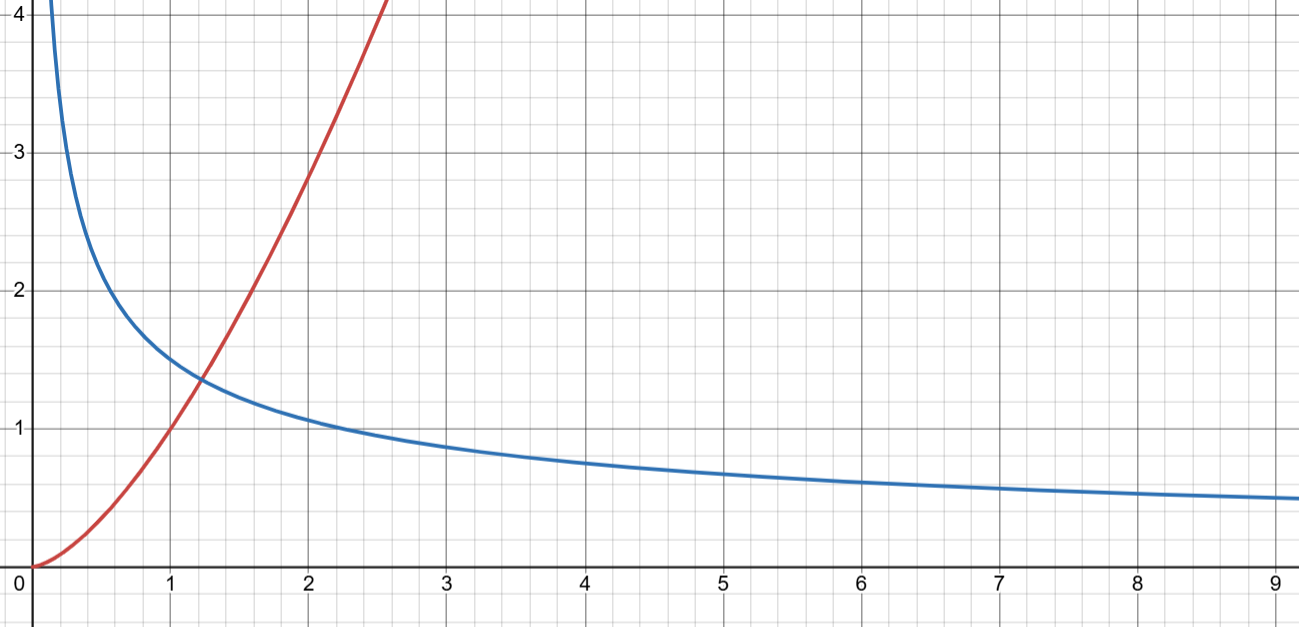
verkar som jag fått nån skärningspunkt här

Arup skrev:Fick lite tips från livehjälpen.
Där smög det sig in ett fel.
Derivatan av är , inte .
Men eftersom x-värdet var 1 så blir det samma resultat på y'(1), vilket betyder att svaret ändå blev rätt.
Förstod du tillvägagångssättet?
Arup skrev:Så här ser funktionen och dess derivata ut
Det verkar konstigt. Vilken funktion?
yYngve skrev:Arup skrev:Så här ser funktionen och dess derivata ut
Det verkar konstigt. Vilken funktion?
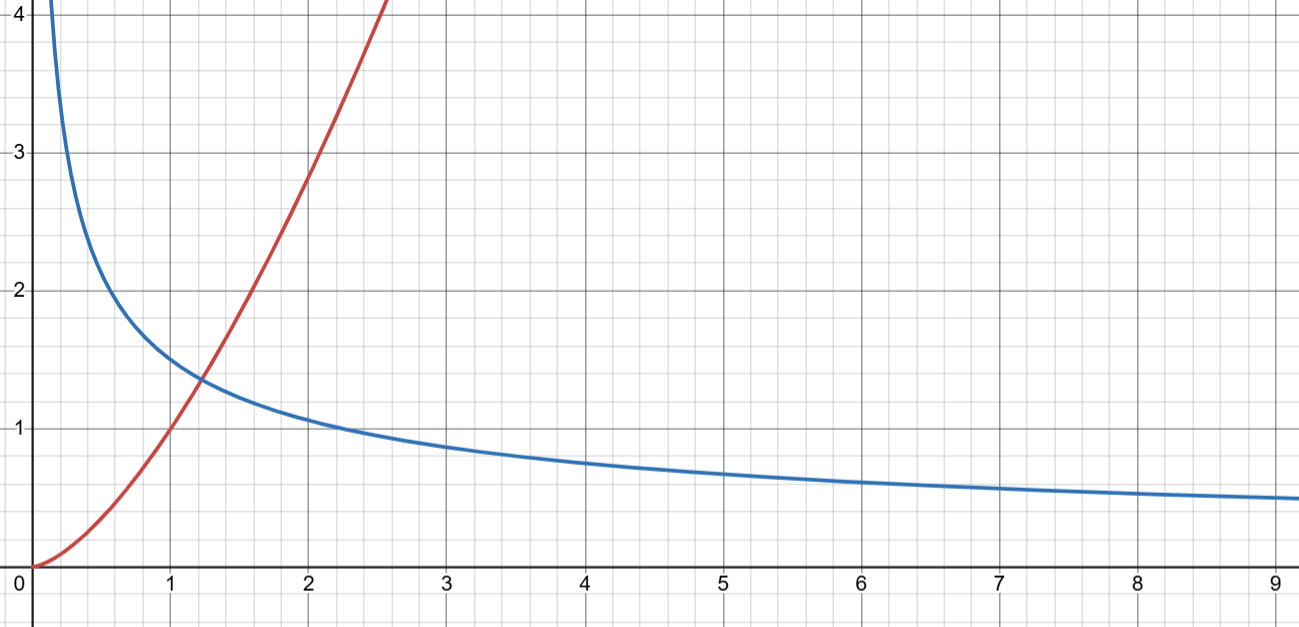
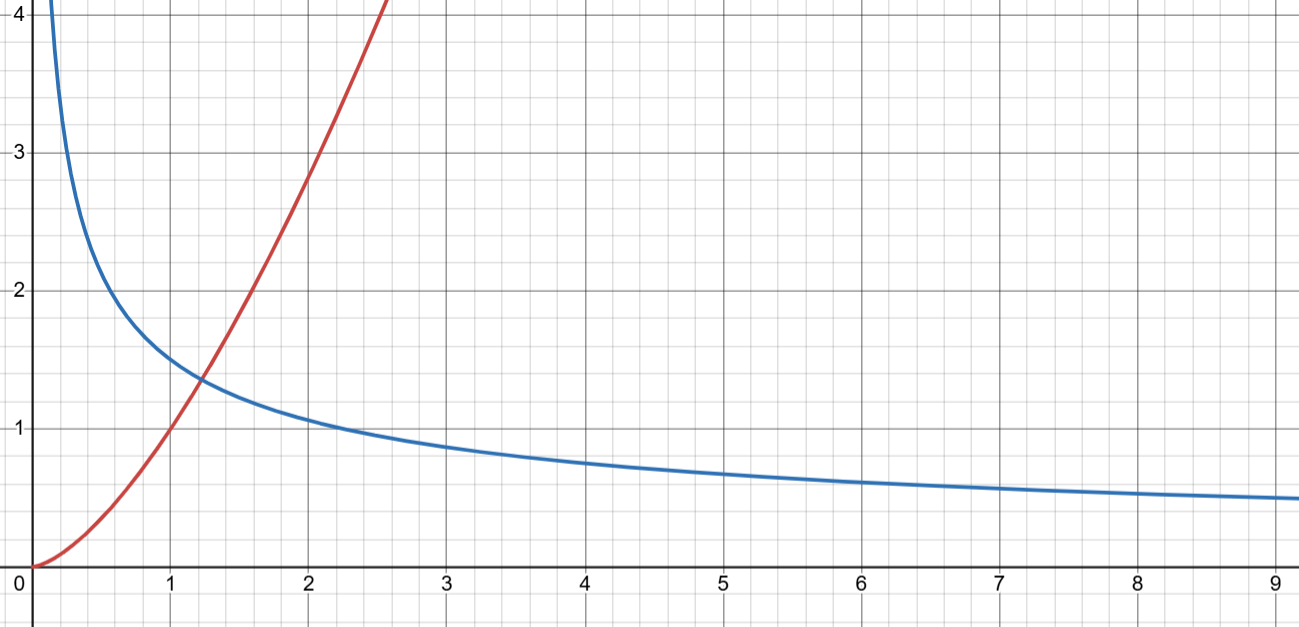
och dess derivata
jag tror vi fick fel svar rätt borde väl vara att man ska utgå från koordinaterna
Man får använda både f(1) och f'(1).
Arup skrev:
och dess derivata
Nej, det stämmer inte.
Så här ser och dess derivata ut:
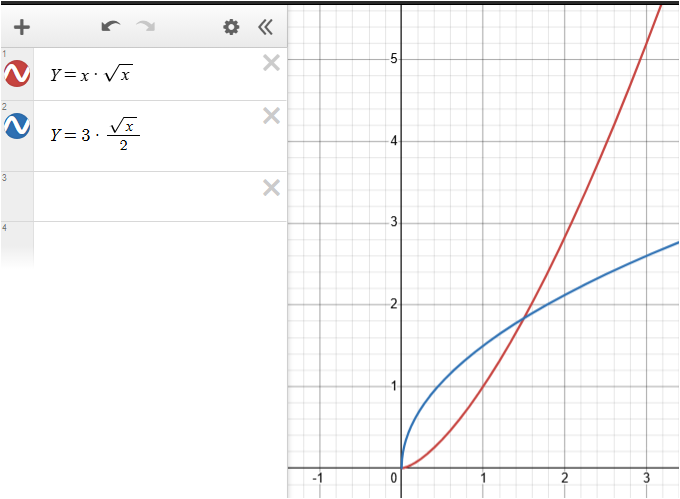
Sedan är skärningspunkten mellan dessa funktioner inte relevant, dvs lösningen till ekvationen hjälper oss inte att lösa uppgiften.
Arup skrev:jag tror vi fick fel svar rätt borde väl vara att man ska utgå från koordinaterna
Nej, rätt svar är y = -6x+4.
- Punkten (1, -3) ligger på grafen till y = f'(x)
- Punkten (1, -2) ligger på grafen till y = f(x)
Vet du hur du ska kunna se skillnad på graferna?
Yngve skrev:Arup skrev:jag tror vi fick fel svar rätt borde väl vara att man ska utgå från koordinaterna
Nej, rätt svar är y = -6x+4.
- Punkten (1, -3) ligger på grafen till y = f'(x)
- Punkten (1, -2) ligger på grafen till y = f(x)
Vet du hur du ska kunna se skillnad på graferna?
Nej. Skulle du kunna förklara ?
Tillägg: 26 dec 2025 22:33
Eller det har att göra med hur den originella funktionen dvs förhåller sig till dess derivata
Arup skrev:[...]
Tillägg: 26 dec 2025 22:33
Eller det har att göra med hur den originella funktionen dvs förhåller sig till dess derivata
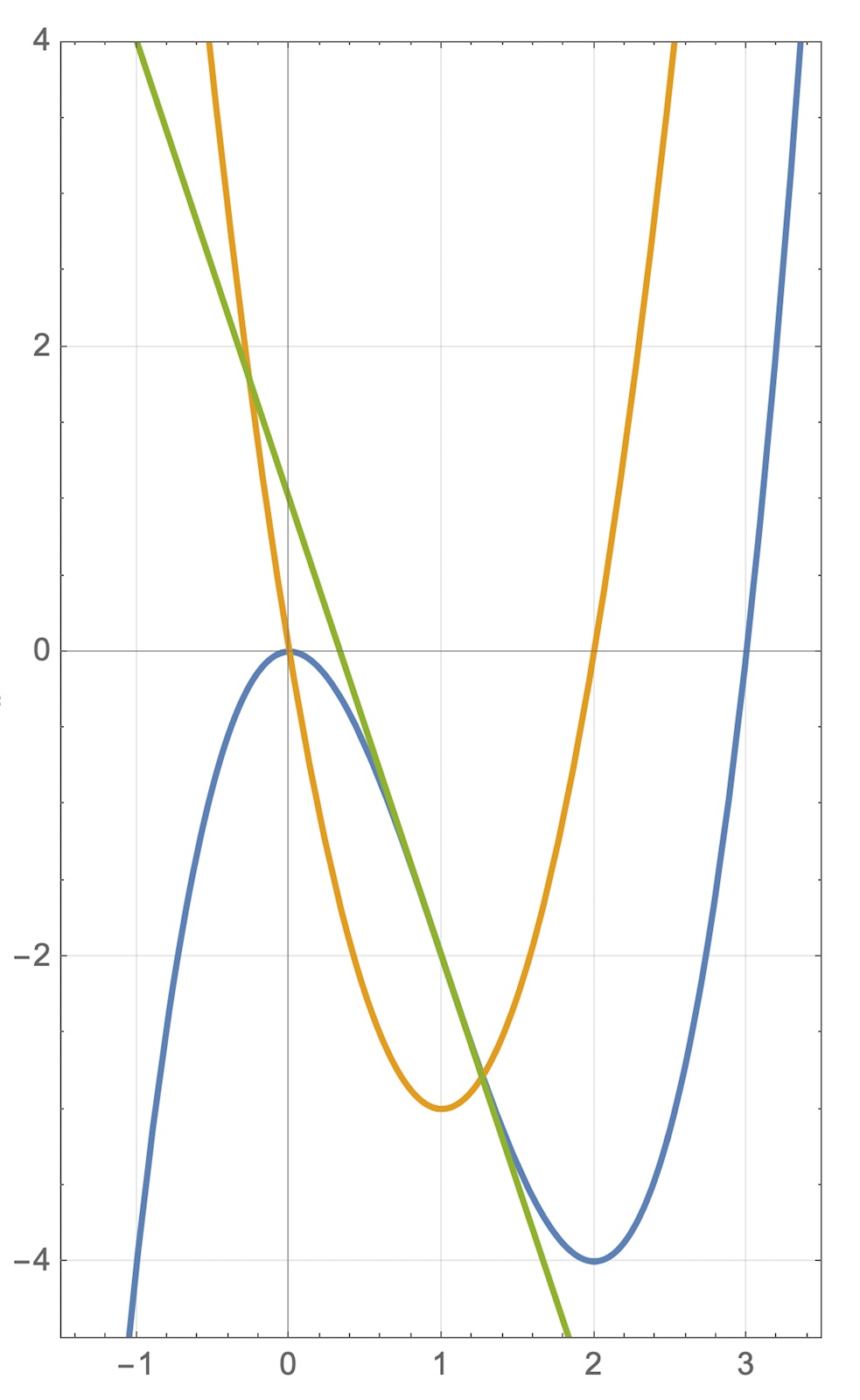
Ja, för att lösa uppgiften behöver vi kunna särskilja graferna y = f(x) och y = f'(x) ur denna bild, där jag har kallat graferna A och B:
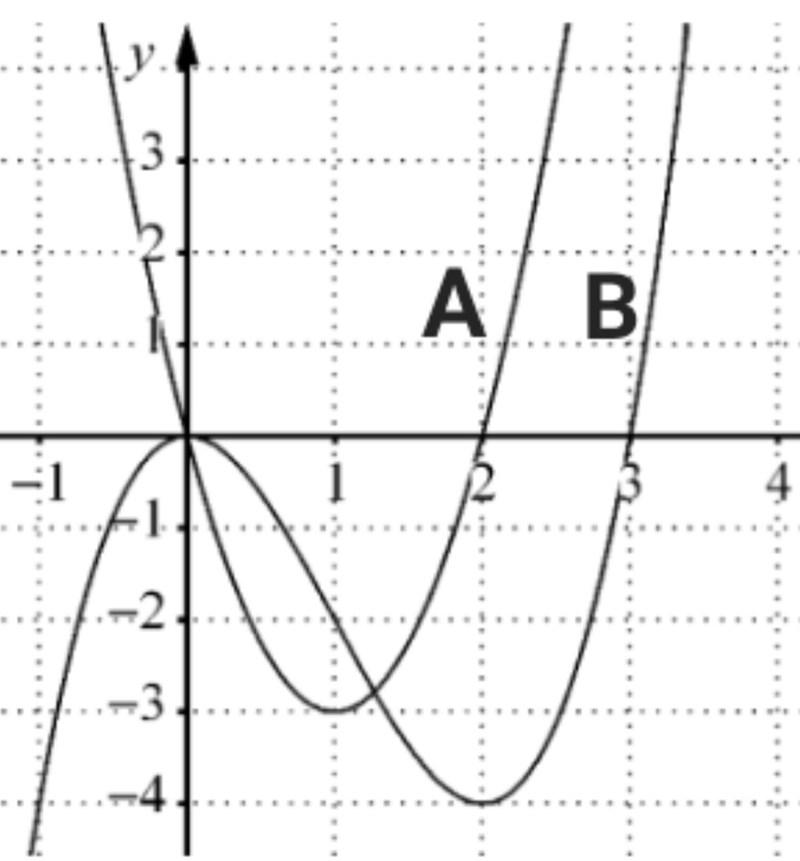
Vi ser att graf A passerar x-axeln på två ställen.
Vi ser att graf B har horisontell tangent vid samma x-koordinater.
Det omvända gäller inte.
Därför är graf A derivatan y = f'(x) och graf B är y = f(x).
=====
Ytterligare samband:
Graf A har positiva y-värden där graf B har positiv lutning och negativa y-värden där graf B har negativ öutning.
Det omvända gäller inte.
Därför är graf A derivatan y = f'(x) och graf B är y = f(x).
==========
Hängde du med?
Yngve skrev:Arup skrev:[...]
Tillägg: 26 dec 2025 22:33
Eller det har att göra med hur den originella funktionen dvs förhåller sig till dess derivata
Ja, för att lösa uppgiften behöver vi kunna särskilja graferna y = f(x) och y = f'(x) ur denna bild, där jag har kallat graferna A och B:
Vi ser att graf A passerar x-axeln på två ställen.
Vi ser att graf B har horisontell tangent vid samma x-koordinater.
Det omvända gäller inte.
Därför är graf A derivatan y = f'(x) och graf B är y = f(x).
=====
Ytterligare samband:
Graf A har positiva y-värden där graf B har positiv lutning och negativa y-värden där graf B har negativ öutning.
Det omvända gäller inte.
Därför är graf A derivatan y = f'(x) och graf B är y = f(x).
==========
Hängde du med?
Ja, men jag förstår inte vad du menar med" "
"
Var i bilden ser jag det ?
Arup skrev:Ja, men jag förstår inte vad du menar med"
"
Var i bilden ser jag det ?
Här har jag i blått ritat in de två horisontella tangenterna till graf B:
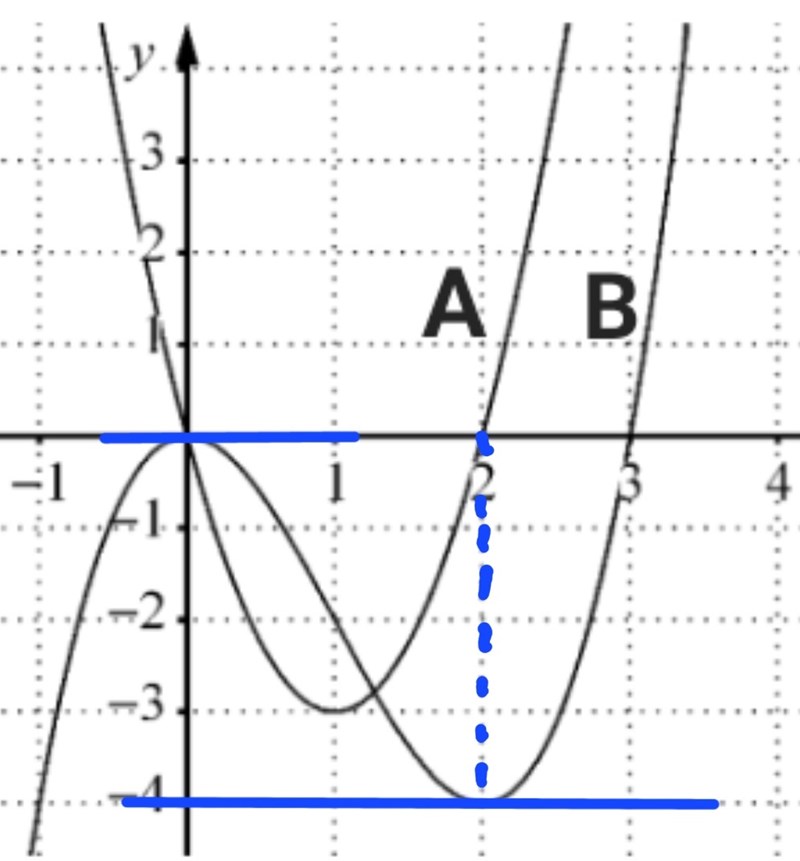
Tangeringspunkterna har samma x-koordinater som nollställena till graf A, nämligen vid x = 0 och x = 2.