Bestäm tankens höjd och radie så att dess volym blir så stor som möjligt.

Man kan rita tak och cylinder i genomskärning i två dimensioner så blir det lättare att se vilka variabler man ska införa. 

Jag vet inte hur jag ska göra.

Rita taket så som det ser ut sett från gaveln på huset.

Okej, så här ritade jag den.

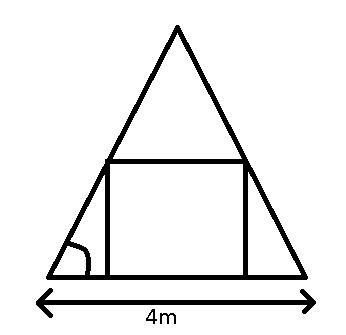
Vilken volym har cylindern, om radien är r och höjden är h?

Med tanke på taket, vilket värde är det största h kan ha om radien är r?

Volymen för cylindern är $V=\mathrm{\pi }·{\mathrm{r}}^2·\mathrm{h}$.

Största h-et  har jag ingen aning om.

Det bör räcka med Ma2 för att ta fram höjden som en funktion av cylinderns radie.

Du vet också längden på takets lutande sidor eftersom du har fått en vinkel i triangeln. 

Vi kan få höjden och takets lutande sidor med trigonometri.

$\frac{h}{2}=\tan \left(60\right) \Rightarrow h=2\tan \left(60\right)=3,46...m$

$\frac{2}{x}=\cos \left(60\right) \Rightarrow x=\frac{2}{\cos {\displaystyle (}{\displaystyle 60}{\displaystyle )}}=4 m$

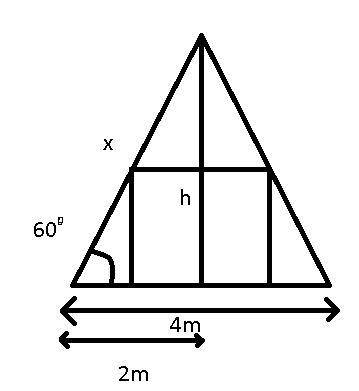
Det kan vi, men just vinkeln 60 grader gör att triangeln är liksidig, för då är alla vinklar 60 grader. 

Använd likformighet för att beräkna h som en funktion av r. Triangeln ovanför tanken är likformig med hela vinden.

Jag skrev såhär:

$\frac{H}{h}=\frac{R}{r}\Rightarrow H=\frac{hR}{r}$

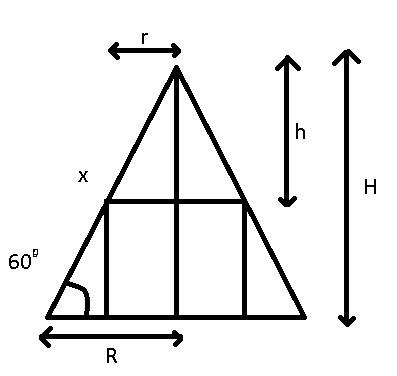
Du vet att 2R = 4,0 m. Hur stort är H?

Varför kallar du höjden i den lilla triangeln för samma sak om vi redan börjat använda för tankens höjd? Det kommer att bli jätterörigt med en variabel som betyder två olika saker.