Bestäm täthetsfunktionen för Z (Matematik/Universitet/Sannolikhet och Statistik)

Såhär långt kom jag men körde fast för hur jag ska bestämma gränserna då z-x är mellan 0 och 1/2

Någon? Är fortfarande fast på detta problem 🥲

Vad säger lösningsförslaget?

Jag förstår inte hur du resonerade dig fram till gränserna 1,2? När man faltar funktionerna måste man tänka på att den ena integralen förskjuts $z-u$ . Beroende lite på hur du väljer att lösa problemet kommer du få olika gränser för din faltningsintegral. Men på något sätt måste du hantera de två intervallen $1<z<3/2$ och $z>3/2$

Jag skulle föreslå att du använder Heavyside-funktionen (om ni lärt er dem). Det kan göra det mer mekaniskt (automatiskt) att hantera gränserna.

Funktionerna kan då uttryckas som

$\displaystyle f_X\left(x\right)=\frac{5\mathrm{\Theta}[x-1]}{x^6}$ (Lever på intervallet >1)

$\displaystyle f_Y\left(x\right)=2\left(\mathrm{\Theta}\left[x\right]-\mathrm{\Theta}\left[x-\frac12\right]\right)$ (Lever på intervallet 0 till 1/2)

Nu vill du alltså beräkna faltningsintegralen

$\displaystyle f_{X+Y}\left(z\right)=\int_{-\infty}^{\infty}f_X\left(u\right)f_Y\left(z-u\right)\,\mathrm{d}u$

Med Heavysidefunktionens räkneregler får du gränsförenklingarna nästan "automatiskt"

D4NIEL skrev:
Jag förstår inte hur du resonerade dig fram till gränserna 1,2? När man faltar funktionerna måste man tänka på att den ena integralen förskjuts $z-u$ . Beroende lite på hur du väljer att lösa problemet kommer du få olika gränser för din faltningsintegral. Men på något sätt måste du hantera de två intervallen $1<z<3/2$ och $z>3/2$

Jag skulle föreslå att du använder Heavyside-funktionen (om ni lärt er dem). Det kan göra det mer mekaniskt (automatiskt) att hantera gränserna.

Funktionerna kan då uttryckas som

$\displaystyle f_X\left(x\right)=\frac{5\mathrm{\Theta}[x-1]}{x^6}$ (Lever på intervallet >1)

$\displaystyle f_Y\left(x\right)=2\left(\mathrm{\Theta}\left[x\right]-\mathrm{\Theta}\left[x-\frac12\right]\right)$ (Lever på intervallet 0 till 1/2)

Nu vill du alltså beräkna faltningsintegralen

$\displaystyle f_{X+Y}\left(z\right)=\int_{-\infty}^{\infty}f_X\left(u\right)f_Y\left(z-u\right)\,\mathrm{d}u$

Med Heavysidefunktionens räkneregler får du gränsförenklingarna nästan "automatiskt"

Hm heavysidefunktionen känner jag tyvärr inte till och den har jag aldrig lärt mig. Men jag känner igen faltningsformeln och det är den lösningsförslaget använde sig av, dock förstår jag inte hur man resonerar med gränserna.

destiny99 skrev:
D4NIEL skrev:
Jag förstår inte hur du resonerade dig fram till gränserna 1,2? När man faltar funktionerna måste man tänka på att den ena integralen förskjuts $z-u$ . Beroende lite på hur du väljer att lösa problemet kommer du få olika gränser för din faltningsintegral. Men på något sätt måste du hantera de två intervallen $1<z<3/2$ och $z>3/2$

Jag skulle föreslå att du använder Heavyside-funktionen (om ni lärt er dem). Det kan göra det mer mekaniskt (automatiskt) att hantera gränserna.

Funktionerna kan då uttryckas som

$\displaystyle f_X\left(x\right)=\frac{5\mathrm{\Theta}[x-1]}{x^6}$ (Lever på intervallet >1)

$\displaystyle f_Y\left(x\right)=2\left(\mathrm{\Theta}\left[x\right]-\mathrm{\Theta}\left[x-\frac12\right]\right)$ (Lever på intervallet 0 till 1/2)

Nu vill du alltså beräkna faltningsintegralen

$\displaystyle f_{X+Y}\left(z\right)=\int_{-\infty}^{\infty}f_X\left(u\right)f_Y\left(z-u\right)\,\mathrm{d}u$

Med Heavysidefunktionens räkneregler får du gränsförenklingarna nästan "automatiskt"

Hm heavysidefunktionen känner jag tyvärr inte till och den har jag aldrig lärt mig. Men jag känner igen faltningsformeln och det är den lösningsförslaget använde sig av, dock förstår jag inte hur man resonerar med gränserna.

Bättre att publicera lösningsförslsget och markera det du undrar över så kan säkert ngn förklara

Trinity2 skrev:
destiny99 skrev:
D4NIEL skrev:
Jag förstår inte hur du resonerade dig fram till gränserna 1,2? När man faltar funktionerna måste man tänka på att den ena integralen förskjuts $z-u$ . Beroende lite på hur du väljer att lösa problemet kommer du få olika gränser för din faltningsintegral. Men på något sätt måste du hantera de två intervallen $1<z<3/2$ och $z>3/2$

Jag skulle föreslå att du använder Heavyside-funktionen (om ni lärt er dem). Det kan göra det mer mekaniskt (automatiskt) att hantera gränserna.

Funktionerna kan då uttryckas som

$\displaystyle f_X\left(x\right)=\frac{5\mathrm{\Theta}[x-1]}{x^6}$ (Lever på intervallet >1)

$\displaystyle f_Y\left(x\right)=2\left(\mathrm{\Theta}\left[x\right]-\mathrm{\Theta}\left[x-\frac12\right]\right)$ (Lever på intervallet 0 till 1/2)

Nu vill du alltså beräkna faltningsintegralen

$\displaystyle f_{X+Y}\left(z\right)=\int_{-\infty}^{\infty}f_X\left(u\right)f_Y\left(z-u\right)\,\mathrm{d}u$

Med Heavysidefunktionens räkneregler får du gränsförenklingarna nästan "automatiskt"

Hm heavysidefunktionen känner jag tyvärr inte till och den har jag aldrig lärt mig. Men jag känner igen faltningsformeln och det är den lösningsförslaget använde sig av, dock förstår jag inte hur man resonerar med gränserna.

Bättre att publicera lösningsförslsget och markera det du undrar över så kan säkert ngn förklara

Aa ok. Här är lösningsförslaget nedan:

Några frågor gällande detta:

1) varför integrerar man map på dy och inte dx när man skriver upp faltningsformeln? Dessutom gäller den formeln om X och Y är oberoende har jag för mig vilket inte nämnts något om i lydelsen.

2) var får de z>=3/2 som gäller i intervallet [0,1/2] för Y?

3) jag undrar också var 1<=z<=3/2 kommer ifrån samt gränserna 0 till z-1?

4) varför integrerar man för z>=3/2 samt 1<=z<=3/2?

1) Man kan lika gärna integrera med avseende på x. Sedan har du rätt att uppgiften inte säger något om oberoende utan det får man nog bara anta, fördelningen inte entydigt bestämd annars.

Fråga 2) 3) och 4) hänger alla ihop. Eftersom 0<=y<=1/2 och 1<=X och Z=X+Y så får vi två olika alternativ, antingen är Z>=3/2 och då kan Y vara vad som helst i sitt utfallsrum, exempelvis om Z=4 så kan Y anta vilket värde som helst mellan 0 och 1/2, X är ju då någonstans mellan 3½ och 4. Om däremot Z är mindre 3/2 säg Z=1,2 då kan inte Y vara säg 0,3, utan då har vi Y i intervallet 0 till 0,2, eller mer precis i intervallet 0 till Z-1.

Smutsmunnen skrev:
1) Man kan lika gärna integrera med avseende på x. Sedan har du rätt att uppgiften inte säger något om oberoende utan det får man nog bara anta, fördelningen inte entydigt bestämd annars.

Fråga 2) 3) och 4) hänger alla ihop. Eftersom 0<=y<=1/2 och 1<=X och Z=X+Y så får vi två olika alternativ, antingen är Z>=3/2 och då kan Y vara vad som helst i sitt utfallsrum, exempelvis om Z=4 så kan Y anta vilket värde som helst mellan 0 och 1/2, X är ju då någonstans mellan 3½ och 4. Om däremot Z är mindre 3/2 säg Z=1,2 då kan inte Y vara säg 0,3, utan då har vi Y i intervallet 0 till 0,2, eller mer precis i intervallet 0 till Z-1.

Jag känner inte att jag förstår dina svar på 2) 3) och 4) helt. Jag förstår att x>=1 för X då. men förstår inte hur man kommer på z>=3/2 samt 1<=z<=3/2 och sen var gränsen 0 till z-1 kommer ifrån.

Hur går det? :)

Det går bra tack!

Jag vet inte hur jag ska förklara bättre.

Som jag skrev

"Eftersom 0<=y<=1/2 och 1<=X och Z=X+Y så får vi två olika alternativ, antingen är Z>=3/2 och då kan Y vara vad som helst i sitt utfallsrum, exempelvis om Z=4 så kan Y anta vilket värde som helst mellan 0 och 1/2, X är ju då någonstans mellan 3½ och 4. Om däremot Z är mindre 3/2 säg Z=1,2 då kan inte Y vara säg 0,3, utan då har vi Y i intervallet 0 till 0,2, eller mer precis i intervallet 0 till Z-1."

Uppdelningen i fall mellan Z>=3/2 eller ej bygger alltså på att om Y i så fall kan anta alla värden i sitt utfallsrum, i annat fall ej.

Jag tror du får förklara bättre vad du inte förstår.

Smutsmunnen skrev:
Det går bra tack!

Jag vet inte hur jag ska förklara bättre.

Som jag skrev

"Eftersom 0<=y<=1/2 och 1<=X och Z=X+Y så får vi två olika alternativ, antingen är Z>=3/2 och då kan Y vara vad som helst i sitt utfallsrum, exempelvis om Z=4 så kan Y anta vilket värde som helst mellan 0 och 1/2, X är ju då någonstans mellan 3½ och 4. Om däremot Z är mindre 3/2 säg Z=1,2 då kan inte Y vara säg 0,3, utan då har vi Y i intervallet 0 till 0,2, eller mer precis i intervallet 0 till Z-1."

Uppdelningen i fall mellan Z>=3/2 eller ej bygger alltså på att om Y i så fall kan anta alla värden i sitt utfallsrum, i annat fall ej.

Jag tror du får förklara bättre vad du inte förstår.

Ja asså jag förstår inte hur man kommer fram till att z>=3/2 samt 1<=z<=3/2. Det kanske kommer från definitionsmängd eller värdemängd tankesätt som inte nämns i lösningen (oklart). Du pratar om utfallsrum för X och Y, jag är lite osäker på vad du menar med det. Innebär utfallsrum typ värdemängd elr definitionsmängd? X är [1,inf) och Y[0,1/2]. Då är väl Z =[1,1/2] U [1/2, inf)? Jag kan vara ute och cyklar men det är kanske så de resonerar.

Jag skall försöka titta på det ikväll, men Smutsmunnen har kanske sagt vad som kan sägas. Jag skall se om jag ev. kan ge någon alternativ vinkel på det.

Trinity2 skrev:
Jag skall försöka titta på det ikväll, men Smutsmunnen har kanske sagt vad som kan sägas. Jag skall se om jag ev. kan ge någon alternativ vinkel på det.

Tack snälla! det har fortfarande inte klarnat dessvärre men jag väntar på svar.

Jag gör ett tappert försök att förklara.

Facit har valt att beräkna faltningsintegralen

$\displaystyle f_Z\left(z\right)=\int_{-\infty}^{\infty}f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u$

Funktionen $f_Y(u)$ är nollskild då $u$ ligger i intervallet 0 till 1/2, oavsett vilket värde $z$ har. Vi kan illustrera området med en zu-graf:

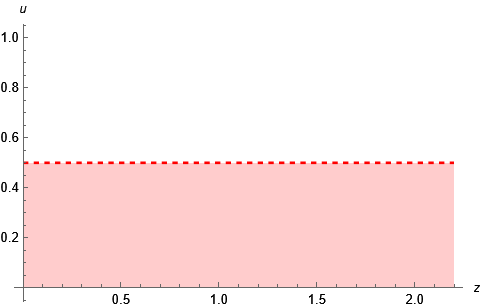Funktionen $f_X(z-u)$ är nollsklld då $1<z-u<\infty$ . Vi kan illustrera området med en andra graf:

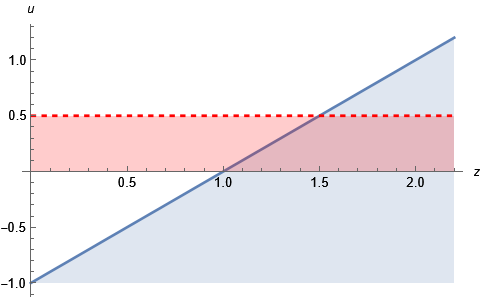
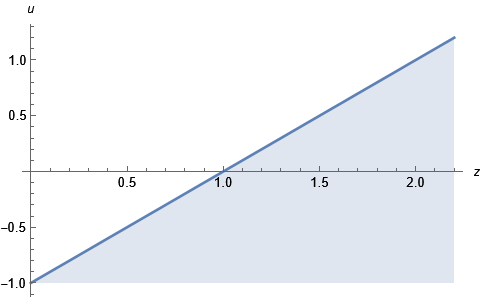Sätter vi ihop villkoren får vi ett mörkrosa område i zu-planet där båda funktionerna är nollskillda samtidigt.

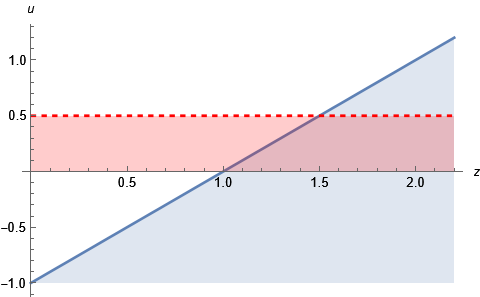
Det mörkrosa området börjar då $z=1$ och efter $z=\frac32$ är det bara ett band mellan $u=0$ och $u=\frac12$ .
I området $1\leq z \leq \frac32$ begränsas $u$ uppåt av linjen $u=z-1$

D4NIEL skrev:
Jag gör ett tappert försök att förklara.

Facit har valt att beräkna faltningsintegralen

$\displaystyle f_Z\left(z\right)=\int_{-\infty}^{\infty}f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u$

Funktionen $f_Y(u)$ är nollskild då $u$ ligger i intervallet 0 till 1/2, oavsett vilket värde $z$ har. Vi kan illustrera området med en zu-graf:

Funktionen $f_X(z-u)$ är nollsklld då $1<z-u<\infty$ . Vi kan illustrera området med en andra graf:

Sätter vi ihop villkoren får vi ett mörkrosa område i zu-planet där båda funktionerna är nollskillda samtidigt.

Det mörkrosa området börjar då $z=1$ och efter $z=\frac32$ är det bara ett band mellan $u=0$ och $u=\frac12$ .
I området $1\leq z \leq \frac32$ begränsas $u$ uppåt av linjen $u=z-1$

Vad står z-u för? och hur får man fram z=1 och z=3/2?

$z-u$ är det facit kallar $z-y$ . För faltningsintegralen ( $Z=X+Y$ , oberoende stokastiska variabler) gäller att

$\displaystyle f_Z\left(z\right)=\int_{-\infty}^{\infty}f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u=\int_{-\infty}^{\infty}f_X\left(v\right)f_Y\left(z-v\right)\mathrm{d}v$

Gränserna för z bestäms av villkoren för att $f_Y$ och $f_X$ ska vara nollskilda. Jag markerar de punkter du undrar över i grafen:

D4NIEL skrev:
$z-u$ är det facit kallar $z-y$ . För faltningsintegralen ( $Z=X+Y$ , oberoende stokastiska variabler) gäller att

$\displaystyle f_Z\left(z\right)=\int_{-\infty}^{\infty}f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u=\int_{-\infty}^{\infty}f_X\left(v\right)f_Y\left(z-v\right)\mathrm{d}v$

Gränserna för z bestäms av villkoren för att $f_Y$ och $f_X$ ska vara nollskilda samtidigt. Jag markerar de punkter du undrar över i grafen:

Men jag ser inte hur z=1 och z=3/2. Löser man någon ekvation? Jag antar att u=y och x=v?

De två frekvensfunktionerna $f_X$ och $f_Y$ är nollskilda då

$1<z-u\\0<u<\frac12$

För $u=0$ ger första olikheten $z=1$ och för $u=\frac12$ blir det $z=1+\frac12=\frac32$ , men du måste ju förstå varför man vill att funktionerna ska vara nollskilda samtidigt och hur man ska använda brytpunkterna till integralgränserna.

D4NIEL skrev:
De två frekvensfunktionerna $f_X$ och $f_Y$ är nollskilda då

$1<z-u\\0<u<\frac12$

För $u=0$ ger första olikheten $z=1$ och för $u=\frac12$ blir det $z=1+\frac12=\frac32$ , men du måste ju förstå varför man vill att funktionerna ska vara nollskilda samtidigt och hur man ska använda brytpunkterna till integralgränserna.

Varför skall funktionerna vara nollskilda samtidigt? Vad menas med brytpunkterna till integralgränserna?

Om någon eller båda funktionerna i integranden är noll på ett intervall blir bidraget från det intervallet noll. Det innebär att du kan förenkla integralen.

Om t.ex. $f_Y(u)$ bara är nollskild på intervallet 0 till 1/2 gäller att integranden är noll över allt annars och att

$\displaystyle \int_{-\infty}^{\infty} f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u=\int_{0}^{\frac12} f_X\left(z-u\right)f_Y\left(u\right)\mathrm{d}u$