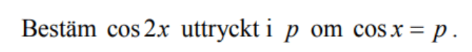Bestäm trig funktion för dubbla vinkeln uttryckt i p

Gäller samma metoder här som https://www.pluggakuten.se/trad/bevis-av-trig-id/ ?

Kan säga att $x={\cos }^{-1}\left(p\right) ?$

I den andra tråden skrev du (alldeles rätt) att 

$\cos \left(2x\right)\hspace{0.17em}=\hspace{0.17em}1-2{\sin }^2\left(x\right)$

Skriv om det där högerledet, och sedan kallar vi cos(x) för  p .

Jag är lite osäker. Blir det $1-p^2 ?$

Tillägg: 18 sep 2025 21:51

Jag vet inte hur jag kan uttrycka p för $\sin \left(x\right)$

Om vi hade kallat sin(x) för t, så hade vi kunnat skriva  1 - 2sin²(x)  som 1 - 2t² 

Men nu har vi valt att kalla cos(x) för p.

Vet vi något om samband mellan p och t? 

Bubo skrev:

Om vi hade kallat sin(x) för t, så hade vi kunnat skriva  1 - 2sin²(x)  som 1 - 2t² 

Men nu har vi valt att kalla cos(x) för p.

Vet vi något om samband mellan p och t? 

Kan jag skapa ett ekvationssystem med två okända variabler ?

Det behövs inte.

En fråga: Vet vi ett samband mellan p och t?

Samma fråga: Vet vi ett samband mellan cos(x) och sin(x)?

ja jag kan ju utnyttja formlerna för dubbla vinkeln för både sinus och cosinus.

Du har ett uttryck för cos(2x) , det som jag hämtade från din andra tråd. Men det uttrycket innehåller sin(x), inte cos(x). Kan du skriva om det uttrycket så att det innehåller cos(x) och inte sin(x) ?

Bubo skrev:

Du har ett uttryck för cos(2x) , det som jag hämtade från din andra tråd. Men det uttrycket innehåller sin(x), inte cos(x). Kan du skriva om det uttrycket så att det innehåller cos(x) och inte sin(x) ?

Jag tror nog att det här är lösningen du vill att jag skulle komma fram till:

Just det. Snyggt.