Bestäm Trig värdet

Så här har jag resonerat kring frågan

Det finns en enklare väg, som jag kan beskriva senare, men din metod borde också fungera. Dock är sista två raderna fel: det står sin(4v), men i högerledet är det 4v du har.

Jag förstår. Men hur får jag det till $\sin \left(4v\right) ?$

Arup skrev:

Jag förstår. Men hur får jag det till $\sin \left(4v\right) ?$

om v=26.55 så är sin(4v)=sin(4*26.55)

Med tanke på att uppgiften klassificerats under Matematik 4, så undrar jag om det inte är meningen att man bestämmer sinusvärdena (det finns två möjliga svar) m.h.a. trigonometriska formler utan att behöva ta fram själva vinkeln v? På så sätt skulle svaret inte drabbas av tidiga avrundningar.

I så fall är formeln för sinus av dubbla vinkeln samt den trigonometriska ettan högst relevanta. Det kanske blir enklare att se hur dessa ska användas om du börjar med en enkel substitution: $u = 2v$. Efter den här substitutionen så lyder uppgiften:

• Bestäm $\sin 2u$  om  $\cos u = 0.6$

Arup skrev:

Så här har jag resonerat kring frågan

[...]

Nu kommer du nog inte att gå vidare med den lösningen, men jag vill ändå påpeka att det (utöver att det ska stå ett $\approx$ istället för =) så är det gulmarkerade fel. Ett sinusvärde är inte en vinkel.

LuMa07 skrev:

Med tanke på att uppgiften klassificerats under Matematik 4, så undrar jag om det inte är meningen att man bestämmer sinusvärdena (det finns två möjliga svar) m.h.a. trigonometriska formler utan att behöva ta fram själva vinkeln v? På så sätt skulle svaret inte drabbas av tidiga avrundningar.

I så fall är formeln för sinus av dubbla vinkeln samt den trigonometriska ettan högst relevanta. Det kanske blir enklare att se hur dessa ska användas om du börjar med en enkel substitution: $u = 2v$. Efter den här substitutionen så lyder uppgiften:

• Bestäm $\sin 2u$  om  $\cos u = 0.6$

Då kan jag väk använda trig 1:an ?

Arup skrev:

LuMa07 skrev:... formeln för sinus av dubbla vinkeln samt den trigonometriska ettan högst relevanta ...

• Bestäm $\sin 2u$  om  $\cos u = 0.6$

Då kan jag väk använda trig 1:an ?

M.h.a. den trigonometriska ettan får du reda på sin u (två möjliga värden fås) och sedan är det bara dubblavinkelns formel för sin 2u.

LuMa07 skrev:

Arup skrev:

Visa föregående citat

LuMa07 skrev:... formeln för sinus av dubbla vinkeln samt den trigonometriska ettan högst relevanta ...

• Bestäm $\sin 2u$  om  $\cos u = 0.6$

Då kan jag väk använda trig 1:an ?

M.h.a. den trigonometriska ettan får du reda på sin u (två möjliga värden fås) och sedan är det bara dubblavinkelns formel för sin 2u.

Då det + eller - eftersom jag tar väl rotenur

Arup skrev:

Då det + eller - eftersom jag tar väl rotenur

Visa gärna dina uträkningar så blir det enklare att hjälpa dig.

Yngve skrev:

Arup skrev:

Då det + eller - eftersom jag tar väl rotenur

Visa gärna dina uträkningar så blir det enklare att hjälpa dig.

Så här

$$\begin{gathered} {\sin }^2\left(x\right)+{\cos }^2\left(x\right)=1 \\ {\sin }^2\left(x\right)=1-{\cos }^2\left(x\right) \\ \sqrt{{\sin }^2\left(x\right)} =\pm \sqrt{1-{\cos }^2\left(x\right)} \\ \sin \left(x\right)=\pm \sqrt{1-{\cos }^2\left(x\right)} \end{gathered}$$

Arup skrev:

Yngve skrev:

Visa föregående citat

Arup skrev:

Då det + eller - eftersom jag tar väl rotenur

Visa gärna dina uträkningar så blir det enklare att hjälpa dig.

Så här

$$\begin{gathered} {\sin }^2\left(x\right)+{\cos }^2\left(x\right)=1 \\ {\sin }^2\left(x\right)=1-{\cos }^2\left(x\right) \\ \sqrt{{\sin }^2\left(x\right)} =\pm \sqrt{1-{\cos }^2\left(x\right)} \\ \sin \left(x\right)=\pm \sqrt{1-{\cos }^2\left(x\right)} \end{gathered}$$

Ser bra ut

Löst!

En sak som kom intuitivt var att $\sin \left(4v\right)=2 \sin \left(2v\right)\cos \left(2v\right)$

Jag undrar varifrån kommer från ?

Jag antar att det har att göra med $\sin \left(2v\right)=2\sin \left(v\right)\cos \left(v\right)$

Arup skrev:

En sak som kom intuitivt var att $\sin \left(4v\right)=2 \sin \left(2v\right)\cos \left(2v\right)$

Jag undrar varifrån kommer från ?

Jag antar att det har att göra med $\sin \left(2v\right)=2\sin \left(v\right)\cos \left(v\right)$

Ja, formeln för dubbla vinkeln sinus lyder sin(2w) = 2sin(w)cos(w).

Detta gäller för alla vinklar w och du kan därför sätta w = 2v, vilket ger dig sin(2•2v) = 2sin(2v)cos(2v), dvs sin(4v) = 2sin(2v)cos(2v).

=====

Snygg lösning i svar #14, men du behöver inte skriva $\pm$ -0,96 på slutet, det räcker med $\pm$ 0,96.

Några små synpunkter:

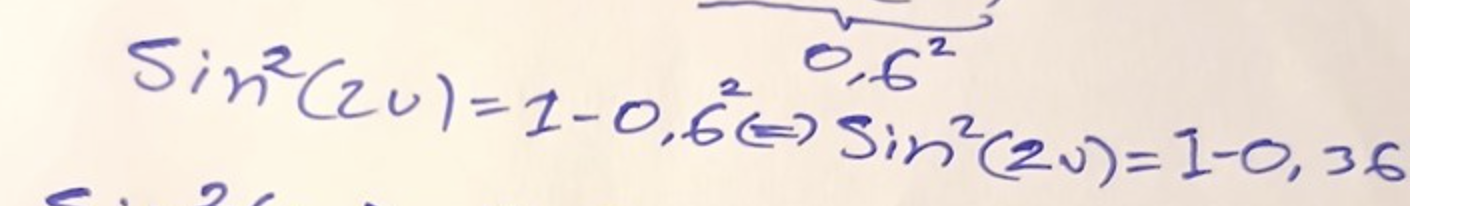
Försök skriva så lite som möjligt:

sin^2(2v)=1-0.6^2=1-0.36=0.64

är inte sant. Tag bort ±.

skrivs bättre =2(±0.8)*0.6

Då vet du vad respektive faktor på radan ovan bidrar med.

Jag undrar kan man inte lösa den enklast genom att lösa ut v från cos(2v)=0,6 genom att ta inversfunktionen/arcos. Sen delar jag båda leden med v för att lösa ut den ?

Arup skrev:

Jag undrar kan man inte lösa den enklast genom att lösa ut v från cos(2v)=0,6 genom att ta inversfunktionen/arcos. Sen delar jag båda leden med v för att lösa ut den ?

Det kommer endast att ge dig ett närmevärde, inte ett exakt svar.

Yngve skrev:

Arup skrev:

Jag undrar kan man inte lösa den enklast genom att lösa ut v från cos(2v)=0,6 genom att ta inversfunktionen/arcos. Sen delar jag båda leden med v för att lösa ut den ?

Det kommer endast att ge dig ett närmevärde, inte ett exakt svar.

Jag förstår inte varför det blir det ? Men även om det skulle bli ett exakt svar skulle jag inte kunna avrunda det för att få ett närmevärde som blir samma sak ?

Arup skrev:

Jag förstår inte varför det blir det ?

Arccos ger närmevärden till alla vinklar, förutom ert fåtal typ 0°, 30°, 45° osv.

Men även om det skulle bli ett exakt svar skulle jag inte kunna avrunda det för att få ett närmevärde som blir samma sak ?

Jovisst kan du avrunda det exakta svaret $\pm0,96$ till färre decimaler, dvs till $\pm1$, men jag förstår inte varför man skulle vilja göra det?

Arup skrev:

Jag undrar kan man inte lösa den enklast genom att lösa ut v från cos(2v)=0,6 genom att ta inversfunktionen/arcos. Sen delar jag båda leden med v för att lösa ut den ?

Denna typ av uppgifter förekommer ofta på den provdel där miniräknare inte är tillåten. Men att kvadrera 0.6 och ta roten ut 0.64 är huvudräkning, liksom grundläggande multiplikation.

Yngve skrev:

Arup skrev:

Visa föregående citat

Jag förstår inte varför det blir det ?

Arccos ger närmevärden till alla vinklar, förutom ert fåtal typ 0°, 30°, 45° osv.

Men även om det skulle bli ett exakt svar skulle jag inte kunna avrunda det för att få ett närmevärde som blir samma sak ?

Jovisst kan du avrunda det exakta svaret $\pm0,96$ till färre decimaler, dvs till $\pm1$, men jag förstår inte varför man skulle vilja göra det?

Jag tycker det känns mer  intuitivt, eftersom det påminer om algebra dvs att lösa ut en variabel dvs x 

Arup skrev:

Jag tycker det känns mer  intuitivt, eftersom det påminer om algebra dvs att lösa ut en variabel dvs x 

Pratar vi fortfarande om för- och nackdelar med att avrunda exakta värden?

Då kan jag tänka mig en del situationer där det faktiskt ger ett mervärde.

Om man t.ex. har beräknat en längd till $3\sqrt{23}$ meter så kan det, beroende på sammanhang, vara bättre att ange detta med hjälp av närmevärdet 14,4 meter eftersom det gör det lättare att förstå och anvönda resultatet.