Bestäm troligt gränsvärde

Hej,

Har fastnat på frågan neden.

Bestämt ett troligt gränsvärde för $\lim_{h \to 0} \frac{10^{3 + h} - 10^{3}}{h}$ .

Jag har löst uppgiften så här

$\lim_{h \to 0} \frac{10^{3 + h} - 10^{3}}{h} = \frac{10^{3 + 0} - 10^{3}}{0} .$ Vilket blir noll i nämnare och det är odefinierat.

Men om jag ersätter h med mycket små värde då kommer det närmer sig talet 2302,85.

exempel $\frac{10^{3 + 0, 0001} - 10^{3}}{0, 0001} = 2302, 850208 \frac{10^{3 + 0, 000000001} - 10^{3}}{0, 000000001} = 2302, 85$

Jag har svarat 2302,82 men det står 0 i facit.

Vad har jag gjort för fel, tacksam om ni svarar.

Står det verkligen noll i facit?

Du ska nog använda derivatans definition och komma på vilken derivata som uttrycket motsvarar, och sedan räkna ut det exakta värdet. Det du gör är förstås en giltig metod för att få ett närmevärde.

Laguna skrev:
Står det verkligen noll i facit?
Du ska nog använda derivatans definition och komma på vilken derivata som uttrycket motsvarar, och sedan räkna ut det exakta värdet. Det du gör är förstås en giltig metod för att få ett närmevärde.

Nej, mitt fel det står f(x)=10^x.
Hur koommer man till 10^x ?

Ställ upp derivatans definition för 10^x så kanske det framgår.

Laguna skrev:
Ställ upp derivatans definition för 10^x så kanske det framgår.

Varför måste jag ställa upp derivatans definition på $10^{X}$ när jag söker svarat till $\lim_{h \to 0} \frac{10^{3 + h} - 10^{3}}{h}$ ?

Laguna skrev:
Ställ upp derivatans definition för 10^x så kanske det framgår.

Jag få noll :(

Hur du kom till tredje raden förstår jag inte, men du kan stanna vid andra raden. Om du sätter x = 3 så har du det sökta uttrycket, eller hur?

Noah skrev:
Laguna skrev:
Ställ upp derivatans definition för 10^x så kanske det framgår.
Jag få noll :(

$\frac{x+h}{h}$ kan inte förkortas till x. (Först tyckte jag det stod "4" men jag förstod av sammanhanget att det var ett "h".)

Smaragdalena skrev:
Noah skrev:
Laguna skrev:
Ställ upp derivatans definition för 10^x så kanske det framgår.
Jag få noll :(
$\frac{x+h}{h}$ kan inte förkortas till x. (Först tyckte jag det stod "4" men jag förstod av sammanhanget att det var ett "h".)

Hur går jag vidare här i från ? Vad gör jag för fel ?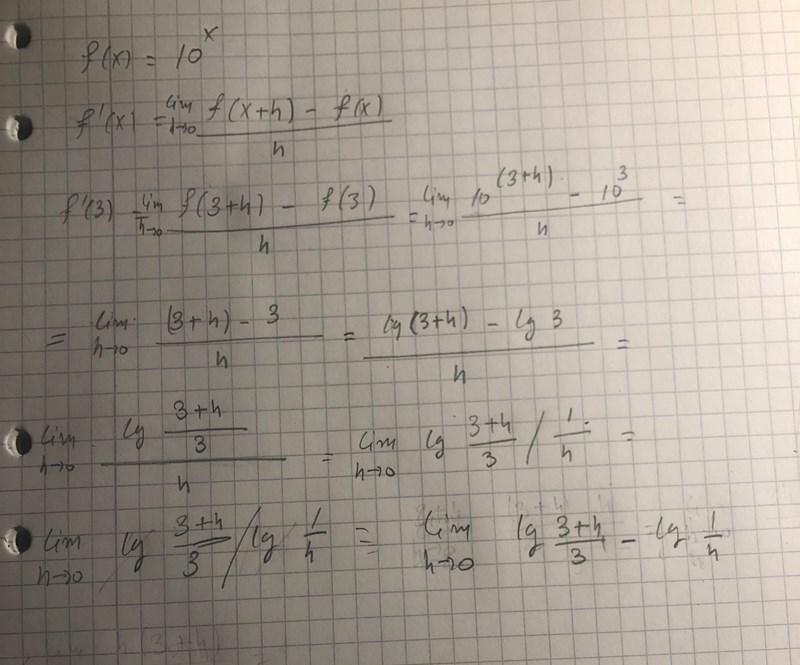

Hej,

Det är fel när du skriver att $\frac{10^{3+h}-10^{3}}{h}$ är samma sak som $\frac{(3+h)-3}{h}.$

Gör såhär istället.

Bryt ut $10^{3}$ i täljaren för att skriva kvoten

$\frac{10^{3+h}-10^{3}}{h} = \frac{10^3\cdot (10^{h}-1)}{h} = 10^{3} \cdot \frac{10^{h}-1}{h}.$

Undersök nu gränsvärdet

$\displaystyle\lim_{h\to 0} \frac{10^{h}-1}{h}.$

Albiki skrev:
Hej,
Det är fel när du skriver att $\frac{10^{3+h}-10^{3}}{h}$ är samma sak som $\frac{(3+h)-3}{h}.$
Gör såhär istället.
Bryt ut $10^{3}$ i täljaren för att skriva kvoten
$\frac{10^{3+h}-10^{3}}{h} = \frac{10^3\cdot (10^{h}-1)}{h} = 10^{3} \cdot \frac{10^{h}-1}{h}.$
Undersök nu gränsvärdet
$\displaystyle\lim_{h\to 0} \frac{10^{h}-1}{h}.$

Tack så mycket :)

Svara

Visa senaste svar