Bestäm värdet på x i olikheten
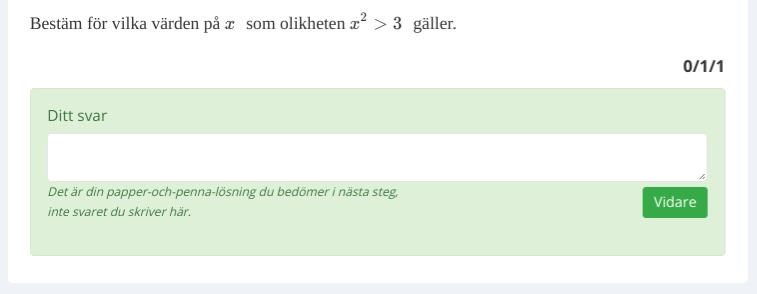 Hej! Jag har kommit fram till rätt svar men förstår inte direkt hur jag ska formulera mig på ett matematiskt språk? Svaret är X > roten ur 3 och x < minus roten ur 3
Hej! Jag har kommit fram till rätt svar men förstår inte direkt hur jag ska formulera mig på ett matematiskt språk? Svaret är X > roten ur 3 och x < minus roten ur 3
Visa hur du kom fram till de svaren så går det säkert bra.
Ja det är väl gott nog om du byter ut och mot eller.
För
Kan säkert skrivas ännu mer matematiskt
Massa skrev:Ja det är väl gott nog om du byter ut och mot eller.
Kan säkert skrivas ännu mer matematiskt
ja exakt men finns det något att sätt att komma fram till svaret, för just nu tänkte jag bara liksom logiskt i huvudet och det är inte direkt någon lösning men skulle man kunna förlänga typ olikeheten för att sedan visa sin uträkning?
ödlan123 skrev:
ja exakt men finns det något att sätt att komma fram till svaret, för just nu tänkte jag bara liksom logiskt i huvudet och det är inte direkt någon lösning men skulle man kunna förlänga typ olikeheten för att sedan visa sin uträkning?
Olikheter är luriga, det är lätt att tänka fel.
Två metoder du kan använda:
Metod 1:
Ersätt olikhetstecknet med ett likhetstecken och lös ekvationen . Du får då de två lösningarna och . Dessa två nollställen delar in tallinjen i tre intervall:
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket är större än . Alltså gäller olikheten i hela detta intervall.
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket inte är större än . Alltså gäller inte olikheten i detta intervall.
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket är större än . Alltså gäller olikheten i hela detta intervall.
Metod 2:
Rita följande två grafer i ett koordinatsystem: Parabeln och den horisontella linjen .
Olikheten är uppfylld för alla där parabeln ligger ovanför den horisontella linjen.
Yngve skrev:ödlan123 skrev:ja exakt men finns det något att sätt att komma fram till svaret, för just nu tänkte jag bara liksom logiskt i huvudet och det är inte direkt någon lösning men skulle man kunna förlänga typ olikeheten för att sedan visa sin uträkning?
Olikheter är luriga, det är lätt att tänka fel.
Två metoder du kan använda:
Metod 1:
Ersätt olikhetstecknet med ett likhetstecken och lös ekvationen . Du får då de två lösningarna och . Dessa två nollställen delar in tallinjen i tre intervall:
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket är större än . Alltså gäller olikheten i hela detta intervall.
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket inte är större än . Alltså gäller inte olikheten i detta intervall.
- . Kontrollera om olikheten gäller här. Välj t.ex. . Då är , vilket är större än . Alltså gäller olikheten i hela detta intervall.
Metod 2:
Rita följande två grafer i ett koordinatsystem: Parabeln och den horisontella linjen .
Olikheten är uppfylld för alla där parabeln ligger ovanför den horisontella linjen.
Ok, tack!



