Bestäm vektorerna
Hej!
Jag har lite svårt att komma igång med följande uppgift: Det enda jag har kommit på är att man möjligtvis kan skriva att:
Det enda jag har kommit på är att man möjligtvis kan skriva att:
Men jag vet inte om det är användbart för uträkningen....
Sedan vet man att den spetsiga vinkeln ska vara 30° så möjligtvis att cos(30°)=v1/v2
I divisionen ovan där det står v1 och v2 ska det egentligen så som i första idén men det tog gräsligt lång tid att skriva i detta program, så jag orkade inte skriva mer hehe...
Tack på förhand!
Nej, längden för var och en av dem är 8, inte summan av längderna.
Rita lite i ett koordinatsystem. Jag föreslår att du låter en av vektorerna ligga längs nån av koordinataxlarna.
jaha, fel läst av mig.
Men om jag gör som du sa så har jag lite svårt att veta hur lång jag ska göra den andra vektorn. Jag vet att den ska vara 8, och i 30° vinkel till den andra vektorn som jag ritat på x-axeln, så vet jag inte i vilken punkt den slutar i. Jag försöker komma på något matematiskt metod för att komma fram till det, men kan inte komma på något.
KlmJan skrev:jaha, fel läst av mig.
Men om jag gör som du sa så har jag lite svårt att veta hur lång jag ska göra den andra vektorn. Jag vet att den ska vara 8, och i 30° vinkel till den andra vektorn som jag ritat på x-axeln, så vet jag inte i vilken punkt den slutar i. Jag försöker komma på något matematiskt metod för att komma fram till det, men kan inte komma på något.

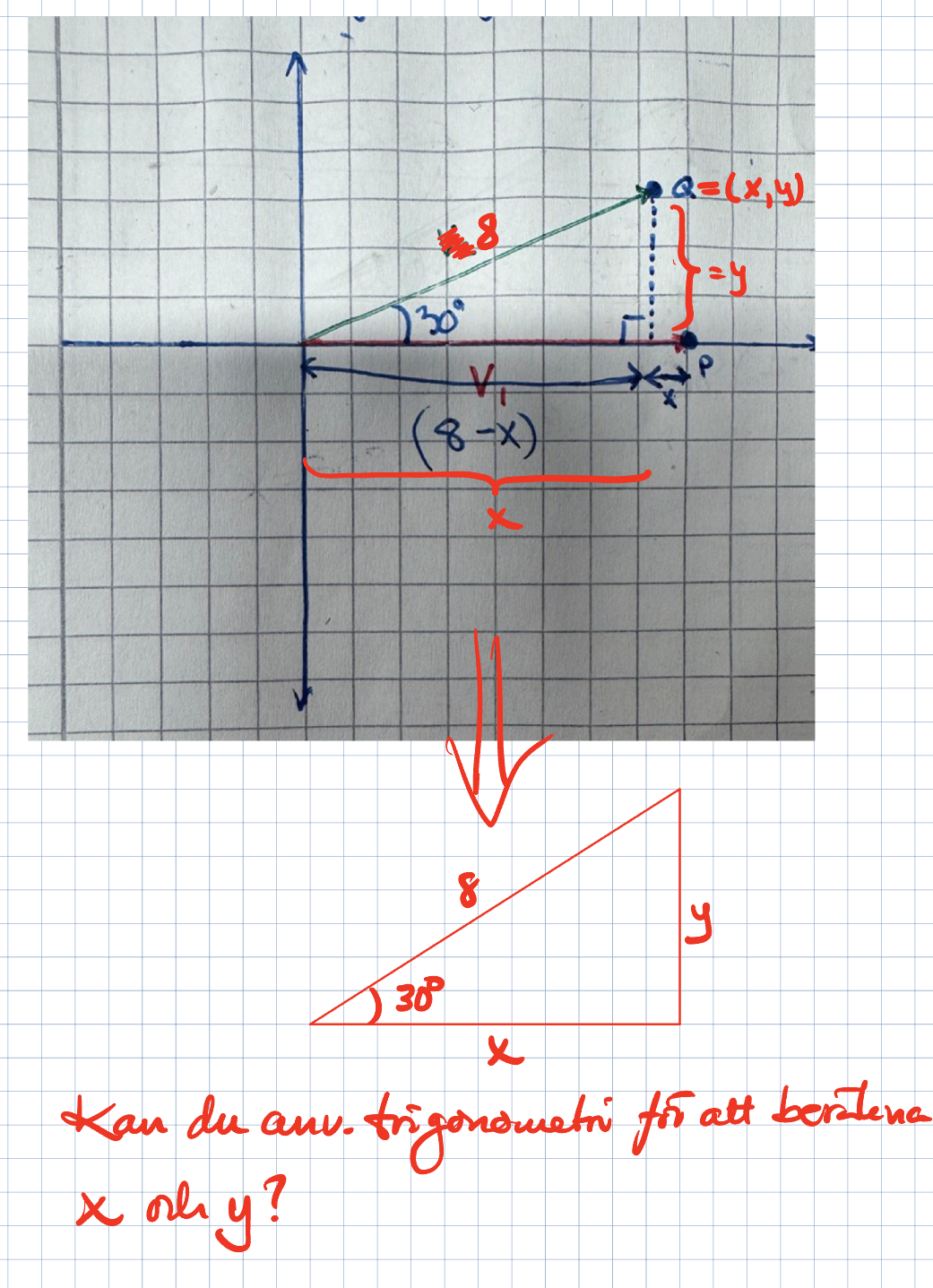
Jag förstår var du vill komma med din fråga. Det kan jag nog lösa. Men innan det har jag en fråga. Hur vet du att punkten Q ligger just i den punkten? eller har du bara satt in en vektor i en random vinkel men med samma längd som den blåa vektorn? Jag vet inte hur jag ska kunna dra den rätta höjden om jag inte vet exakt var punkten Q ligger.
Vi kan placera vektorerna hur som helst, så länge alpha=30°
Här väljer vi en enkel lösning som Laguna föreslog, vi lägger blå längs x-axeln.
Alpha=30°
Då blir punkten Q fixerad. Tänk dig att blå vektor är en dörr karm och röd är dörren. Så öppnar du dörren 30°. Dörrens läge är därmed bestämd.
Vad kan du dra för höjd för att få en rätvinklig triangel i bilden?
Vad kan du dra för höjd för att få en rätvinklig triangel i bilden?
Kan vara fel, men jag tänkte från punkten Q till x-axeln.
KlmJan skrev:Vad kan du dra för höjd för att få en rätvinklig triangel i bilden?
Kan vara fel, men jag tänkte från punkten Q till x-axeln.
EXAKT! Rita och berätta mera för oss! Vad kan du säga om längden på den röda vektorn? Sätt ut siffran på rätt ställe och ersätt alpha med 30°
Här är så långt jag kommit med bilden. Jag kom på att man kan skiva ett uttryck för den delen av vektorn V1 som bildar basen för den rätvinkliga triangeln. Sedan kan man se att höjden är strax över 3 men exakt vet jag inte.
man kanske hade kunnat användarsidan av tangens på något vis. Högst osäker dock.

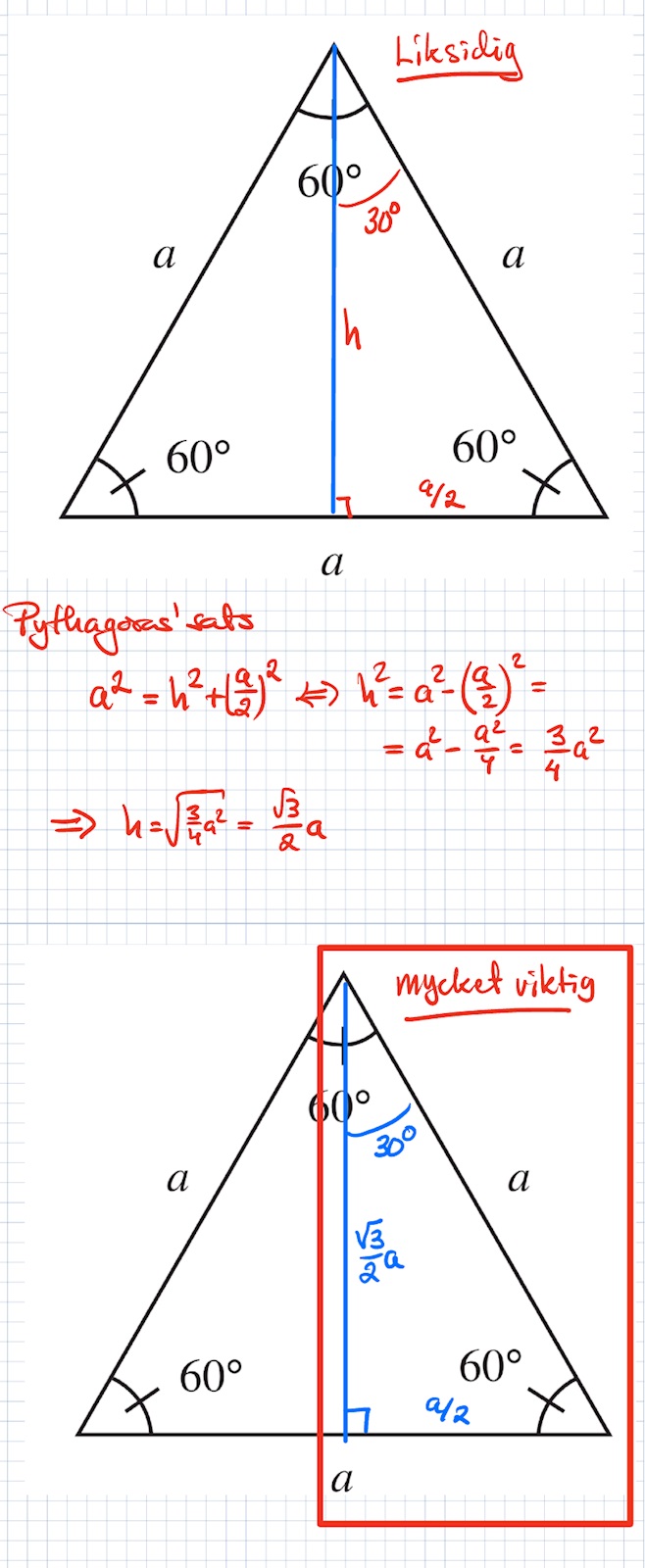
OBS! En triangel med vinkel 30° och 90° ger att den andra vinkeln är ????? Och vad kallar vi en spdan triangel och vad vet vi om dess sidor. Det är en mycket känd triangel.
Den andra vinkeln är 60.
Vill minnas att sidorna har förhållandena x:x sqr3:2x
KlmJan skrev:Den andra vinkeln är 60.
Vill minnas att sidorna har förhållandena x:x sqr3:2x
stämmer
förhållandt är
1 : 1/2 : sqrt3/2
Det blev en gnutta rörigt nu, men orkade inte skriva rent. Här är min lösning:

Det är en bra trig.lösning. Läraren kommer dock att kräva att cos(30°) och sin(30°) anges med sqrt3/2 och 1/2. Det är välkända värden som återkommer hela tiden. Försök memorera dessa. De grundar sig på en 30-60-90-triangel (halv liksidig triangel) och pythagoras sats.
Tack! Ok, ska försöka komma ihåg det :)
Läraren kommer dock att kräva att cos(30°) och sin(30°) anges med sqrt3/2 och 1/2.
Hur hade det sett ut uttryckt i själva lösningen? Har aldrig sett det användas tidigare, därav frågan.
KlmJan skrev:Tack! Ok, ska försöka komma ihåg det :)
Läraren kommer dock att kräva att cos(30°) och sin(30°) anges med sqrt3/2 och 1/2.
Hur hade det sett ut uttryckt i själva lösningen? Har aldrig sett det användas tidigare, därav frågan.
Jag tror du har ett kapitel/avsnitt om 30-60-90-trianglar i din bok. De är så pass viktiga att de alltid ingår i kurser. När man arbetat med dessa vet man direkt att cos(30)=sqrt3/2 och sin(30)=1/2. Efter ett tag blir det en ren flex. Det är dit du bör komma för det spar mycket tid och beräkningar.
Det finns säkert videor på YouTube men jag kunde inte finna någon bra. De pladdrar på i alla riktningar och överkomplicerar saker.
Tack!