Bestäm vikten som maximerar dagsinkomsten av kräftor

Hej!

Jag har lite problem med en uppgift angående tillämpning av derivata där jag ska beräkna vikt respektive kilopris som maximerar en fiskares inkomst vid försäljning av kräftor.

Här är uppgiften:

Detta är så långt jag kommit:

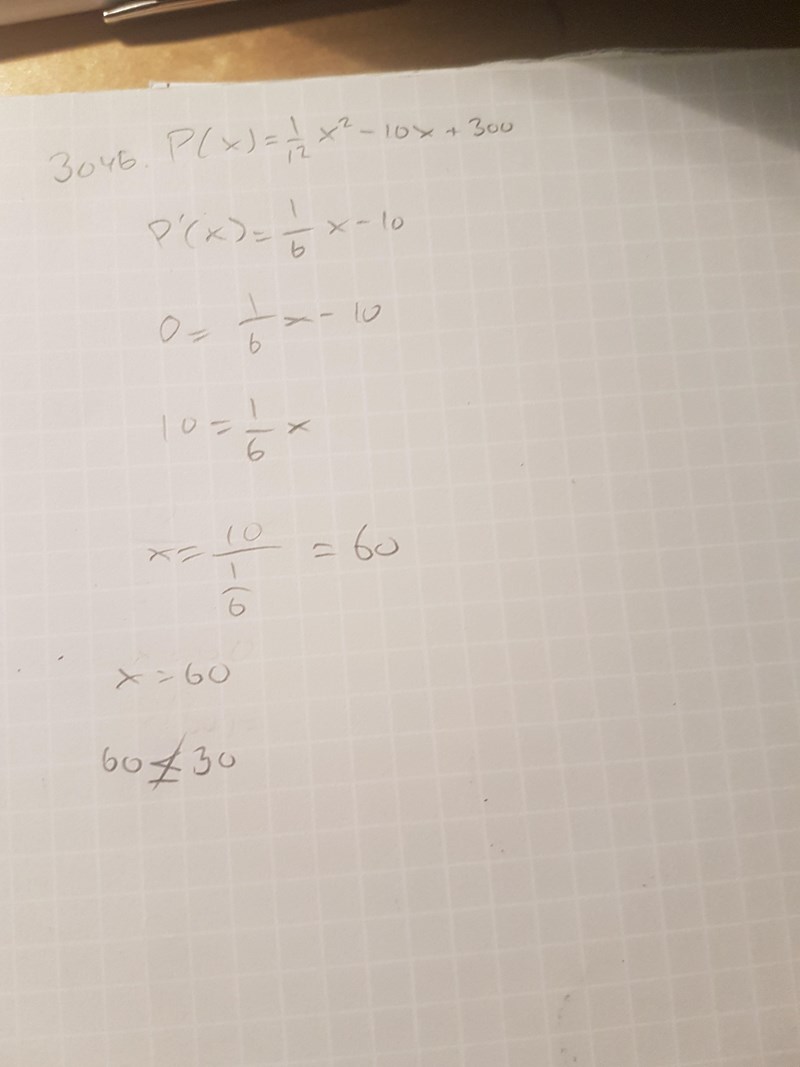
Problemet är att jag inte direkt hittar ett minimi- eller maximivärde mellan intervallet som efterfrågas.

Jag skulle uppskatta lite hjälp.

Tack :)

Det är inte priset du skall maximera, det är inkomsten. Hur stor är inkomsten om fiskaren fångar och säljer x kg kräftor?

Smaragdalena skrev:
Det är inte priset du skall maximera, det är inkomsten. Hur stor är inkomsten om fiskaren fångar och säljer x kg kräftor?

Blir inte inkomsten då 10x? Tänker jag, eftersom det är det som subtraheras från själva priset.

TheDovah skrev:
Smaragdalena skrev:
Det är inte priset du skall maximera, det är inkomsten. Hur stor är inkomsten om fiskaren fångar och säljer x kg kräftor?
Blir inte inkomsten då 10x? Tänker jag, eftersom det är det som subtraheras från själva priset.

Jag förstår inte vad du menar med att 10x subtraheras från priset.

Tänk så här istället:

Om fiskaren säljer 8 kg kräftor med kilopris 100 kronor per kilo så är inkomsten 8*100 kronor
Om fiskaren säljer 11 kg kräftor med kilopris 90 kronor per kilo så är inkomsten 11*90 kronor
Om fiskaren säljer x kg kräftor med kilopris 110 kronor per kilo så är inkomsten x*110 kronor
Om fiskaren säljer x kg kräftor med kilopris y kronor per kilo så är inkomsten x*y kronor

Kan du då ställa upp ett uttryck för inkomsten om fiskaren säljer x kilo kräftor med kilopris p(x) kronor per kilo?

Yngve skrev:
TheDovah skrev:
Smaragdalena skrev:
Det är inte priset du skall maximera, det är inkomsten. Hur stor är inkomsten om fiskaren fångar och säljer x kg kräftor?
Blir inte inkomsten då 10x? Tänker jag, eftersom det är det som subtraheras från själva priset.
Jag förstår inte vad du menar med att 10x subtraheras från priset.
Tänk så här istället:
Om fiskaren säljer 8 kg kräftor med kilopris 100 kronor per kilo så är inkomsten 8*100 kronor
Om fiskaren säljer 11 kg kräftor med kilopris 90 kronor per kilo så är inkomsten 11*90 kronor
Om fiskaren säljer x kg kräftor med kilopris 110 kronor per kilo så är inkomsten x*110 kronor
Om fiskaren säljer x kg kräftor med kilopris y kronor per kilo så är inkomsten x*y kronor
Kan du då ställa upp ett uttryck för inkomsten om fiskaren säljer x kilo kräftor med kilopris p(x) kronor per kilo?

Jag gjorde det som jag tror att du menade men stötte på ett stort problem...

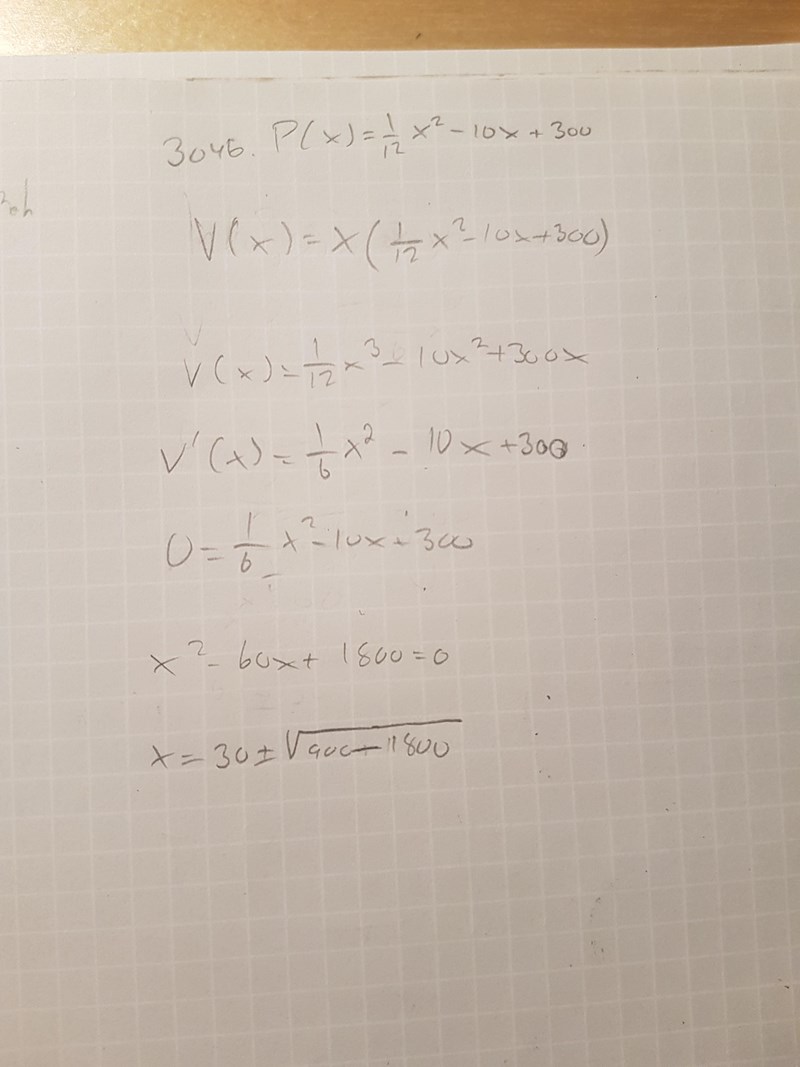
Det kommer att blk ett komplext tal som svar....

TheDovah skrev:
Jag gjorde det som jag tror att du menade men stötte på ett stort problem...
...
Det kommer att blk ett komplext tal som svar....

Ja du gjorde rätt men sen blev det ett slarvfel vid deriveringen:

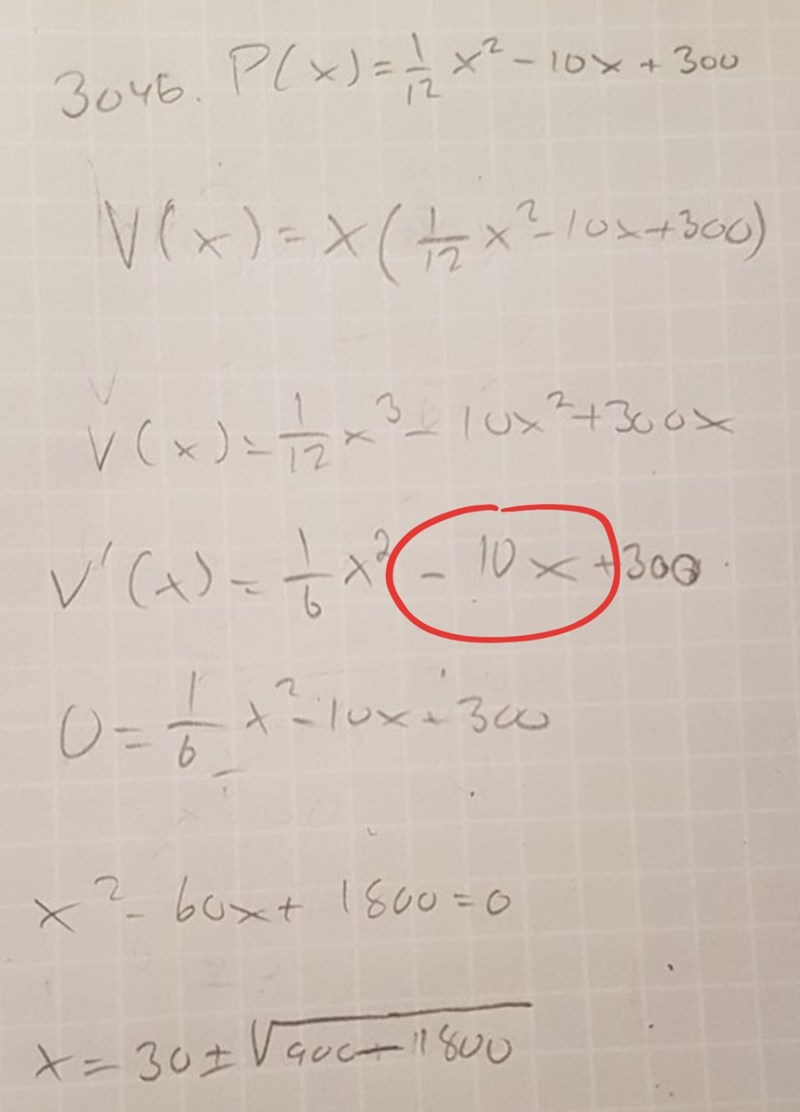
Yngve skrev:
TheDovah skrev:
Jag gjorde det som jag tror att du menade men stötte på ett stort problem...
...
Det kommer att blk ett komplext tal som svar....
Ja du gjorde rätt men sen blev det ett slarvfel vid deriveringen:

Aha!

Jag tror jag löst uppgiften rätt nu: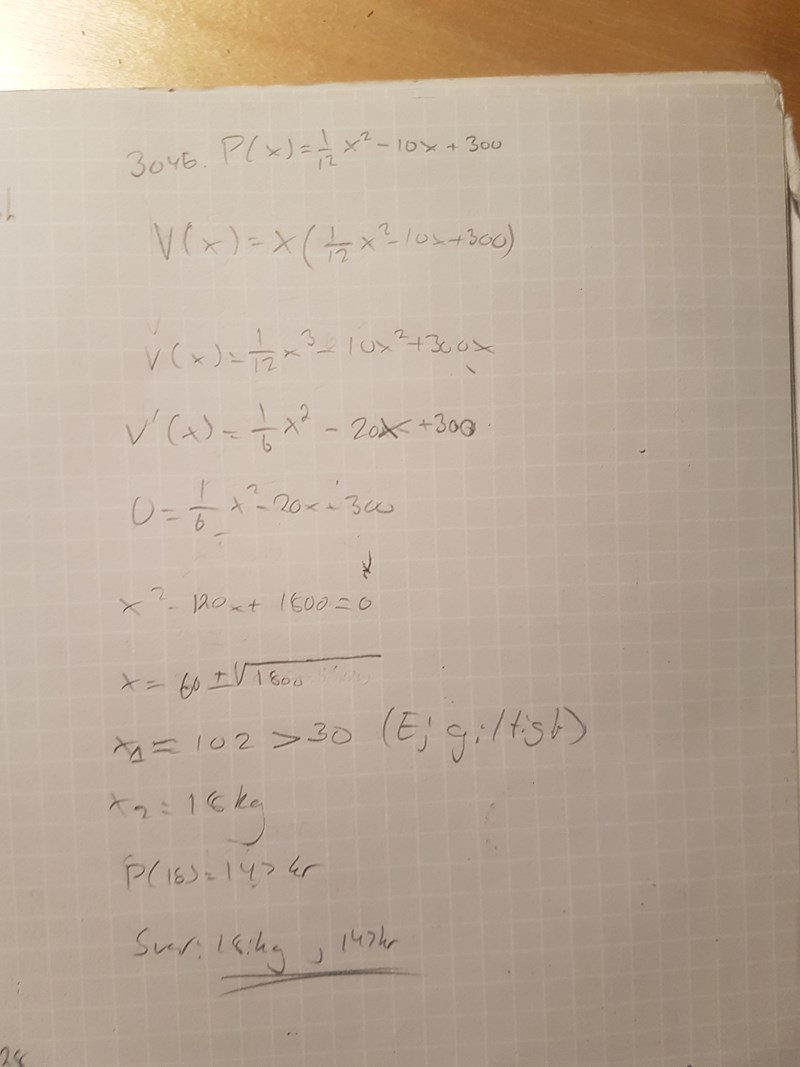

Det står däremot 20kg och 133kr i facit. Kan detta vara pga avrundning?

TheDovah skrev:

Aha!
Jag tror jag löst uppgiften rätt nu:
Det står däremot 20kg och 133kr i facit. Kan detta vara pga avrundning?

Konstigt. Jag tycker att din lösning är rätt. Skillnaden borde inte bero på avrundning.

Det enda jag saknar är ett resonemang kring att den extrempunkt du hittade verkligen är en maxpunkt.

EDIT - Nu ser jag felet. Derivatan av $\frac{1}{12}x^3$ är inte $\frac{1}{6}x^2$ .

Yngve skrev:
TheDovah skrev:
Aha!
Jag tror jag löst uppgiften rätt nu:
Det står däremot 20kg och 133kr i facit. Kan detta vara pga avrundning?
Konstigt. Jag tycker att din lösning är rätt. Skillnaden borde inte bero på avrundning.
Det enda jag saknar är ett resonemang kring att den extrempunkt du hittade verkligen är en maxpunkt.
EDIT - Nu ser jag felet. Derivatan av $\frac{1}{12}x^3$ är inte $\frac{1}{6}x^2$ .

Ah, vad dum jag är! XD Tack för hjälpen! :)

Svara

Visa senaste svar