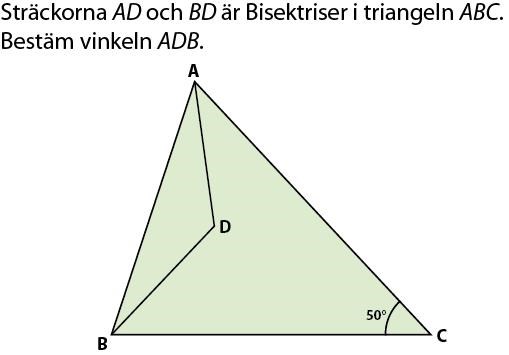
Bestäm vinkel med hjälp av bisektriser (Matematik/Matte 2/Logik och geometri)

När du skriver A respektive B, är det vinklarna BAC respektive ABC?

Du vet att vinklarna BAD och ABD är hälften av BAC respektive ABC. Med hjälp av detta kan du beräkna vinkeln BDA, som man frågar efter.

Visa spoiler

Kalla vinkeln BAD för x. Beräkna vinklarna BAC och ABC uttryckta i x. Beräkna vinkeln ABD. Beräkna till sist vinkeln ADB.

Återigen en geometri-uppgift där så lite är bestämt, att man är fri att bestämma mycket själv.

Bestäm därför att AC är lika lång som BC , dvs att triangeln är likbent med vinklarna 50 65 65

Linjerna AD och BD är bisektriser, så de delar alltså vinklarna 65 grader i två lika delar.
Därmed vet man två av de tre vinklarna i triangeln ABD, och kan lätt beräkna den efterfrågade vinkeln.

larsolof skrev:
Återigen en geometri-uppgift där så lite är bestämt, att man är fri att bestämma mycket själv.
Bestäm därför att AC är lika lång som BC , dvs att triangeln är likbent med vinklarna 50 65 65
Linjerna AD och BD är bisektriser, så de delar alltså vinklarna 65 grader i två lika delar.
Därmed vet man två av de tre vinklarna i triangeln ABD, och kan lätt beräkna den efterfrågade vinkeln.

Det är lite farligt att bara betrakta ett specialfall som är lätt att lösa. Jag blir inte förvånad om man får poängavdrag för det.

Laguna skrev:
larsolof skrev:
Återigen en geometri-uppgift där så lite är bestämt, att man är fri att bestämma mycket själv.
Bestäm därför att AC är lika lång som BC , dvs att triangeln är likbent med vinklarna 50 65 65
Linjerna AD och BD är bisektriser, så de delar alltså vinklarna 65 grader i två lika delar.
Därmed vet man två av de tre vinklarna i triangeln ABD, och kan lätt beräkna den efterfrågade vinkeln.
Det är lite farligt att bara betrakta ett specialfall som är lätt att lösa. Jag blir inte förvånad om man får poängavdrag för det.

Den rätta svaret på frågan, "bestäm vinkeln ADB", måste gälla även för det fall ABC är en likbent triangel.
Triangel ABC kan ha vilken form som helst, bara vinkeln vid hörnet C är 50 grader.
T.ex. kan den vara en rätvinklig triangel 50 90 40. Eller t.ex. 50 120 10.
Den efterfrågade vinkeln vid D blir alltid lika stor oavsett triangelns form.

Kreativitet, att kunna lösa problem, tänka utanför boxen, är viktigare än poäng på matteprov.
Om jag var lärare skulle jag ge extrapoäng till elever som kan hitta genvägar till rätt svar.

larsolof skrev:
Laguna skrev:
larsolof skrev:
Återigen en geometri-uppgift där så lite är bestämt, att man är fri att bestämma mycket själv.
Bestäm därför att AC är lika lång som BC , dvs att triangeln är likbent med vinklarna 50 65 65
Linjerna AD och BD är bisektriser, så de delar alltså vinklarna 65 grader i två lika delar.
Därmed vet man två av de tre vinklarna i triangeln ABD, och kan lätt beräkna den efterfrågade vinkeln.
Det är lite farligt att bara betrakta ett specialfall som är lätt att lösa. Jag blir inte förvånad om man får poängavdrag för det.
Den rätta svaret på frågan, "bestäm vinkeln ADB", måste gälla även för det fall ABC är en likbent triangel.
Triangel ABC kan ha vilken form som helst, bara vinkeln vid hörnet C är 50 grader.
T.ex. kan den vara en rätvinklig triangel 50 90 40. Eller t.ex. 50 120 10.
Den efterfrågade vinkeln vid D blir alltid lika stor oavsett triangelns form.
Kreativitet, att kunna lösa problem, tänka utanför boxen, är viktigare än poäng på matteprov.
Om jag var lärare skulle jag ge extrapoäng till elever som kan hitta genvägar till rätt svar.

Bara om eleverna ser till att visa att det gäller för alla trianglar som stämmer med förutsättingarna, inte bara likbenta. Man kan mycket väl starta med ditt resonemang och lägga till att summan av de båda vinklarna är densamma, även om vinklarna är olika stora. Att bara visa det för en likbent triangel är inte tillräckligt.

Smaragdalena skrev:
larsolof skrev:
Laguna skrev:
larsolof skrev:
Återigen en geometri-uppgift där så lite är bestämt, att man är fri att bestämma mycket själv.
Bestäm därför att AC är lika lång som BC , dvs att triangeln är likbent med vinklarna 50 65 65
Linjerna AD och BD är bisektriser, så de delar alltså vinklarna 65 grader i två lika delar.
Därmed vet man två av de tre vinklarna i triangeln ABD, och kan lätt beräkna den efterfrågade vinkeln.
Det är lite farligt att bara betrakta ett specialfall som är lätt att lösa. Jag blir inte förvånad om man får poängavdrag för det.
Den rätta svaret på frågan, "bestäm vinkeln ADB", måste gälla även för det fall ABC är en likbent triangel.
Triangel ABC kan ha vilken form som helst, bara vinkeln vid hörnet C är 50 grader.
T.ex. kan den vara en rätvinklig triangel 50 90 40. Eller t.ex. 50 120 10.
Den efterfrågade vinkeln vid D blir alltid lika stor oavsett triangelns form.
Kreativitet, att kunna lösa problem, tänka utanför boxen, är viktigare än poäng på matteprov.
Om jag var lärare skulle jag ge extrapoäng till elever som kan hitta genvägar till rätt svar.
Bara om eleverna ser till att visa att det gäller för alla trianglar som stämmer med förutsättingarna, inte bara likbenta. Man kan mycket väl starta med ditt resonemang och lägga till att summan av de båda vinklarna är densamma, även om vinklarna är olika stora. Att bara visa det för en likbent triangel är inte tillräckligt.

Din lösning Smaragdalena som du var först med i denna tråd är såklart utmärkt, och troligen vad de
flesta mattelärare förväntar sig.
Ändå gäller detta: Lösningen på uppgiften måste gälla för alla trianglar som uppfyller alla villkor som
angetts i uppgiften, och en likbent triangel gör det.

Du skrev det själv: Lösningen skall gälla för alla trianglar som uppfyller kriterierna- alltså duger det inte med en lösning som bara handlar om likbenta trianglar.

Tvärtom. Den likbenta triangel 50 65 65 ( liksom alla trianglar 50 X Y) satisfierar kriterierna i uppgiften.
Därför måste alla trianglar med en vinkel 50 grader ge samma/rätt svar på vinkeln ADB.

Nu håller du ju med mig och säger emot dig själv. Nu har du ett resonemang om att alla trianglar med en vinkel som är 50 grader har samma summa för de båda andra vinklarna, även om triangeln inte är likbent.

Såvitt jag förstår använder larsolof ett metaresonemang, dvs. använder information om uppgiften, och inte bara det som står i uppgiften. Det man antar då är att uppgiften har en lösning, och alltså att svaret inte är "tillräcklig information saknas". Eftersom svaret ska vara ett tal, och inte bero av nån variabel, så måste det vara samma svar för alla trianglar som uppfyller kriterierna i uppgiften, och då kan vi välja en som gör beräkningarna enkla.

Såtillvida har larsolof rätt, men det är inte ett matematiskt resonemang.

$∠ B A C = x \Rightarrow ∠ A B C = 130 ° - x \Rightarrow \frac{x}{2} + 65 ° - \frac{x}{2} + ∠ A D B = 180 ° \Leftrightarrow ∠ A D B = 115 °$

Laguna skrev:
Såvitt jag förstår använder larsolof ett metaresonemang, dvs. använder information om uppgiften, och inte bara det som står i uppgiften. Det man antar då är att uppgiften har en lösning, och alltså att svaret inte är "tillräcklig information saknas". Eftersom svaret ska vara ett tal, och inte bero av nån variabel, så måste det vara samma svar för alla trianglar som uppfyller kriterierna i uppgiften, och då kan vi välja en som gör beräkningarna enkla.
Såtillvida har larsolof rätt, men det är inte ett matematiskt resonemang.

Laguna har förstått vad jag har försökt förklara: "Eftersom svaret måste det vara samma svar för alla trianglar som uppfyller kriterierna i uppgiften, och då kan vi välja en triangel som gör beräkningarna enkla."

Då måste man även motivera hur det kommer sig att svaret är lika för alla trianglar. Gör man det är allt väl, gör man inte det har man bara visat ett specialfall.

Smaragdalena skrev:
Då måste man även motivera hur det kommer sig att svaret är lika för alla trianglar. Gör man det är allt väl, gör man inte det har man bara visat ett specialfall.

Det står bara två saker i uppgiften:
1. Det är en triangel
2. En av triangelns vinklar är 50 grader.
Eftersom svaret måste det vara samma svar för alla trianglar som uppfyller dessa två kriterier i uppgiften, så kan vi välja en triangel som gör beräkningarna enkla. Nog måste väl du Smaragdalena inse att det är så?

Om du skriver en rad som motiverar att det gäller för alla tänkbara värden på vinklarna är det OK. Om du endast visar ett specialfall är det inte OK.

Det gäller för alla tänkbara värden på vinklarna A och B.
Och de tänkbara värdena för vinklarna är 0 < A < 130 och 0 < B < 130 valda så att A+B=130.
Vinkeln vid D måste bli ett, och endast ett, gradtal för alla dessa tänkbara värden på A och B
annars är uppgiften inte lösbar.

Vi är helt överens - men du kan inte bara förutsätt att vinklarna A och B är lika utan vidare resonemang.

Det frågan gäller, eller åtminstone det frågan borde gälla, är hur en lärare skulle bedöma en lösning baserad på larsolofs metod.

Skulle eleven

riskera att få poängavdrag på grund av att hen inte visat att lösningen gäller för alla möjliga vinklar vid C?
få full poäng eller till och med chans på extrapoäng eftersom hen påvisar kreativitet och en förmåga att tänka utanför boxen?

Min gissning är att flertalet lärare skulle välja det förstnämnda alternativet.

Om man ser på larsolofs första lösning så skulle den inte ge full poäng utav den anledningen att han bara visar att det gäller i det specialfall att triangeln är likbent. Sedan för han ett resonemang om att för att uppgiften skall vara lösbar måste detta resultat gälla för alla trianglar som uppfyller kriterierna i uppgiften. Vad är det som säger att uppgiften är lösbar? Det är inte ofta men jag har sett uppgifter där facit säger att "uppgiften är inte lösbar med endast given information".

Därför måste man, som Smaragdalena har sagt, visa att lösningen gäller för godtyckliga vinklar vid A och B. När man gjort det kommer man fram till en lösning som är oberoende av vinklarna vid A och B, eller som larsolof nästan är framme vid i sitt senaste inlägg att summan av A och B och därmed summan av A/2 och B/2 är konstant. Då har man ju visat oberoende men behöver heller inte sätta något värde på A och B för att få fram ett värde på den sökta vinkeln.

Att sedan tycka att det är en kreativ lösning och att eleven tänkt utanför boxen finns det väldigt lite utrymme för. Jag måste som lärare förhålla mig till hur de som, på skolverkets uppdrag, konstruerar de nationella proven och rättningsmallarna till dessa ser på poängsättning på en uppgift som denna. Det blir ju väldigt fel om jag som lärare ger en elev poäng för en lösning om jag vet att jag skulle inte kunna göra det på det nationella provet. Jag kan ju inte heller bortse från rättningsmallen på NP då det skulle ta bort syftet med det nationella provet. Med den erfarenhet jag har av de nationella proven så är det på detta sätt rättningsmallen skulle se ut.

Sedan om man behöver visa för godtyckliga vinklar ACB så är det lite av en annan fråga. Jag vet att tidigare (före LGY11) så var de väldigt noggranna att man för att visa MVG kvaliteter så skulle man räkna generellt och sedan sätta in värden på slutet, även om man som i detta fall har ett värde och därmed ett fall givet. Jag har dock en känsla av att detta har minskat en del, där kan jag dock ha fel och det gäller lika mycket nu som då.