Bestäm vinkeln A

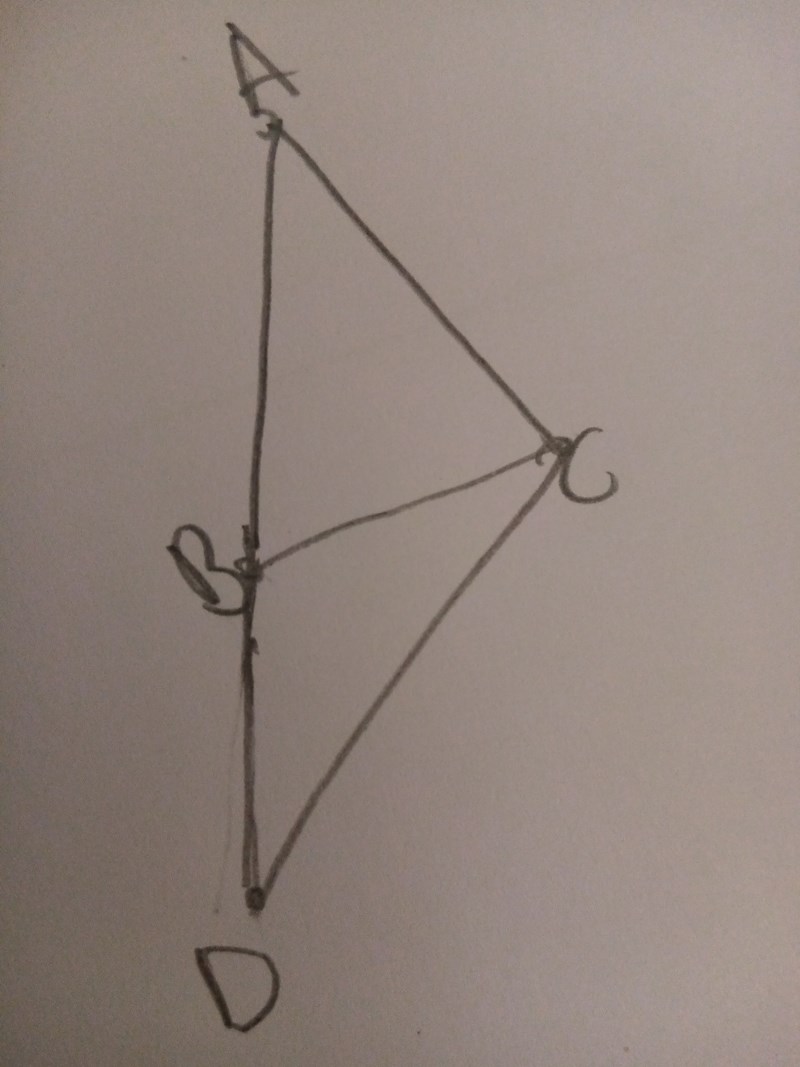
jag försökte att rita figuren men jag vet inte om det är rätt, ser att vi har 3 likbenta trianglar men jag vet inte hur jag ska bestämma vinkeln A
Markera i bilden vilka sidor och vilka vinklar som är lika. Lägg upp en ny bild.
Smaragdalena skrev:Markera i bilden vilka sidor och vilka vinklar som är lika. Lägg upp en ny bild.
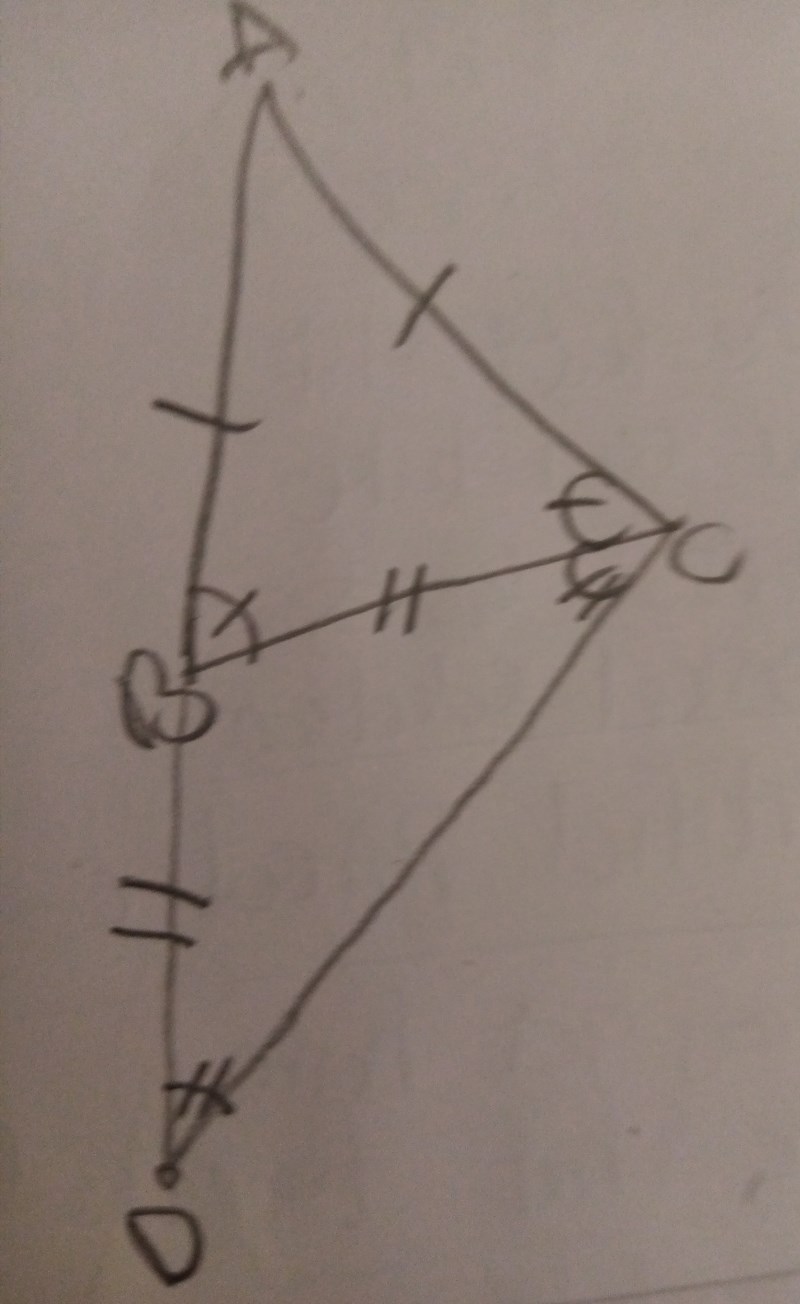
glömde markera att AC = CD
Kan du skriva ett uttryck för vinkeln DBC?
Smaragdalena skrev:Kan du skriva ett uttryck för vinkeln DBC?
180 minus basvinklarna? eller 180 minus ABC
Kalla dina vinklar nånting, exempelvis x och y (man behöver inte alltid vara fantasifull!). Jag förstår inte vad du menar, men det kan vara helt riktigt tänkt. Är det rätt uppfattat att du har kommit på två sätt? Kan du göra en ekvation av det?
Det finns ett mycket enkelt sätt där du inte ens behöver en ekvation.
Kalla vinkeln vid A och de andra två vinklar som är lika stora för x.
Vinkel ABC är yttervinkel till den nedre triangeln, hur stor är den?
Hur stor är då vinkel BCA?
Smaragdalena skrev:Kalla dina vinklar nånting, exempelvis x och y (man behöver inte alltid vara fantasifull!). Jag förstår inte vad du menar, men det kan vara helt riktigt tänkt. Är det rätt uppfattat att du har kommit på två sätt? Kan du göra en ekvation av det?
nu har jag tappat bort mig, förstår inte hur jag ska räkna ut värden när jag inte vet nånting om någon vinkel överhuvudtaget.
Louis skrev:Det finns ett mycket enkelt sätt där du inte ens behöver en ekvation.
Kalla vinkeln vid A och de andra två vinklar som är lika stora för x.
Vinkel ABC är yttervinkel till den nedre triangeln, hur stor är den?
Hur stor är då vinkel BCA?
fast ABC är inte en liksidig triangel så jag kan inte kalla alla vinklar för x
Det är då man inför variabler. Du vet att den första triangeln är likbent, så det finns två vinklar som är lika (kalla dem x) och en tredje vinkel (som du kan räkna ut ett uttryck för med hjälp av vinkelsumman i en triangel). Den nya triangeln är också likbent så det finns två vinklar som du kan kalla y och en tredje vinkel som du kan få fram ett uttryck för.
Kommer du vidare härifrån?
Smaragdalena skrev:Kalla dina vinklar nånting, exempelvis x och y (man behöver inte alltid vara fantasifull!). Jag förstår inte vad du menar, men det kan vara helt riktigt tänkt. Är det rätt uppfattat att du har kommit på två sätt? Kan du göra en ekvation av det?
jag försökte skriva ekvationer men det blev bara fel jag fick x = 360 och en annan gång fick jag x = 0
så här gjorde jag
BAC = y
ABC och ACB är x då de är lika
med yttrevinkelsatsen får vi att CBD = x+y
och BDC samt BCD är var
skriver man ett ekvationssystem med hjälp av triangelns summa som är 180 grader får man inte rätt svar och jag kan inte hitta vad jag gjorde för fel i ekvationerna
Rita upp bilden och sätt ut allt du vet om de olika vinklarna. Lägg upp bilden här, så finns det en chans att vi kan förstå vad det är du gör. Vi som svarar här är bra på matte, men vi är dåliga på tankeläsning.
Smaragdalena skrev:Rita upp bilden och sätt ut allt du vet om de olika vinklarna. Lägg upp bilden här, så finns det en chans att vi kan förstå vad det är du gör. Vi som svarar här är bra på matte, men vi är dåliga på tankeläsning.
.jpg?width=800&upscale=false)
ABC ger dig ett samband mellan x och y.
ACD är likbent, så...
Dr. G skrev:ABC ger dig ett samband mellan x och y.
ACD är likbent, så...
är vinkeln A = ?
Nej, inte 30°. Hur fick du det?
Jag menade att det finns tre vinklar i hela figuren som är x. Eftersom jag redan ritat en figur behåller jag mitt x, fast du kallar vinkeln y. Att den vänstra av 2x-vinklarna i figuren är just så stor följer av yttervinkelsatsen.
Nu framgår genast att x är 1/5 av triangelns vinkelsumma, alltså 180/5.
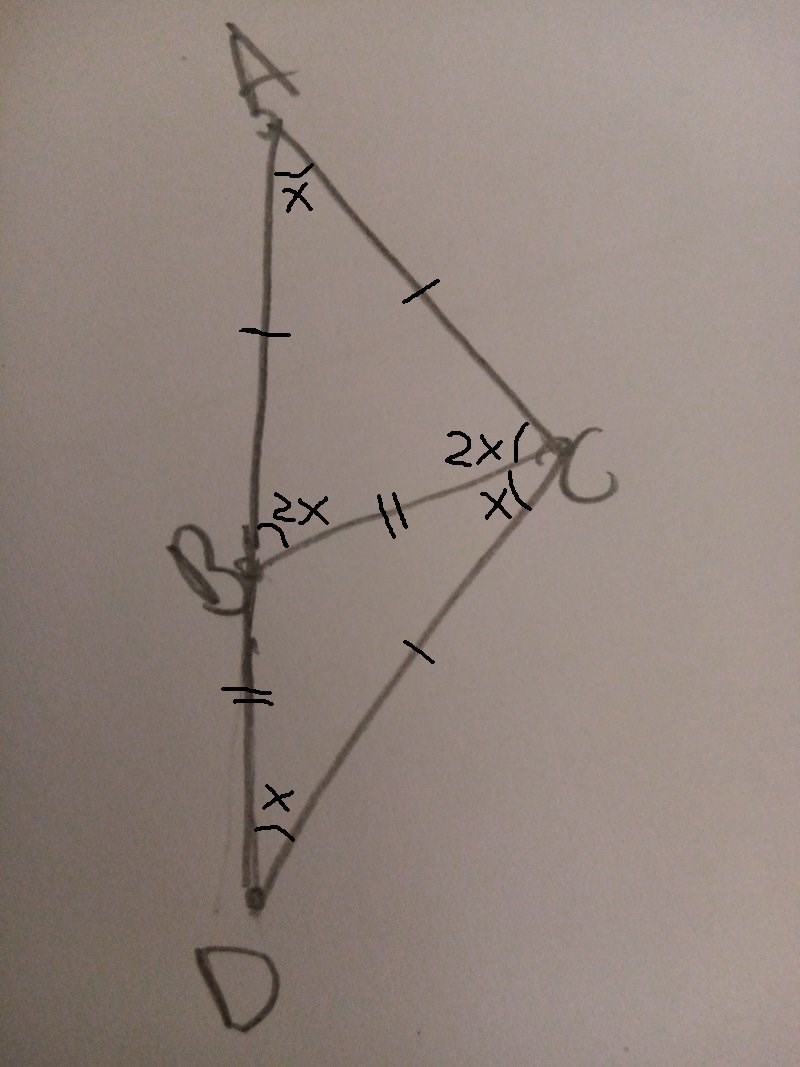
jag förstår dock inte hur sambandet kan stämma?
för när jag testar med en annan likbent triangel, t.ex BAC = 30 då blir basvinklarna 75 var och 30*2 = 60 är inte 75 hur kan det funka i just den triangeln vi har och inte i andra trianglar?
Har du löst ditt ekvationssystem? Då kanske det klarnar.
Louis lösning är elegant.
Dr. G skrev:Har du löst ditt ekvationssystem? Då kanske det klarnar.
Louis lösning är elegant.
jag antar att jag ser varför vi får 2x
Jag kan inte följa med i ditt resonemang. Du kan inte utgå från en triangel där du valt vinklar (fast här förstår jag som sagt inte hur du tänker). Då kan inte alla de givna villkoren varit uppfyllda. Med de villkoren finns bara en uppsättning vinklar.



