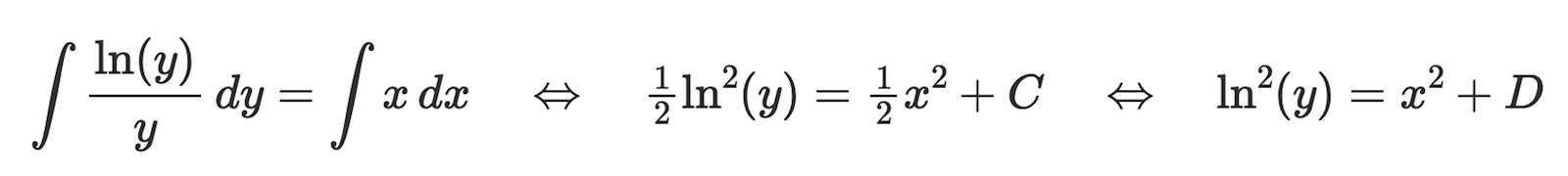bestäm y(0)=e som uppfyller diffekvationen

Trinity2 skrev:

Hur kan u=(ln(y))^2 /2 vara lika med ln(y^2)/2?  Facit gjorde exakt som du gjorde..

(ln(y))^2 =/= ln(y^2) rent allmänt och endast likhet för y=1 eller y=e^2.

Trinity2 skrev:

(ln(y))^2 =/= ln(y^2) rent allmänt och endast likhet för y=1 eller y=e^2.

Jag hänger ej med. Jag gjorde u substitution och fick detta (ln(y))^2/2 efter att jag integrerat u till u^2/2. Facit och du säger ln^2(y)/2 men jag förstår ej

Aha, jag tror jag förstår vad du menar. Det var jag som skrev slarvigt.

Kanske detta är bättre skrivsätt

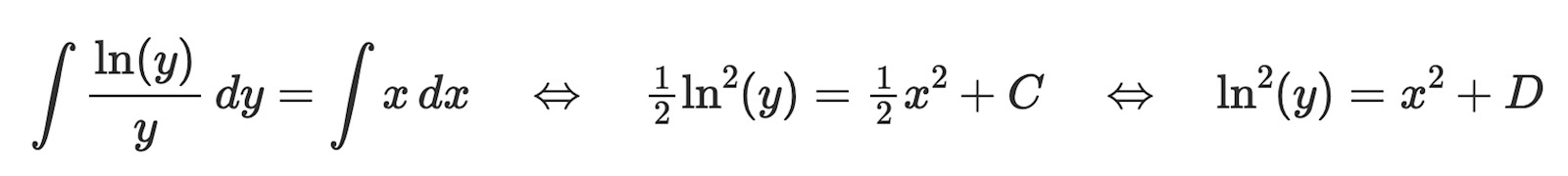
Det är alltså inte y som kvadreras utan ln(y). Jfr med sin^2(x), cos^2(x) etc.

Trinity2 skrev:

Aha, jag tror jag förstår vad du menar. Det var jag som skrev slarvigt.

Kanske detta är bättre skrivsätt

 

Det är alltså inte y som kvadreras utan ln(y). Jfr med sin^2(x), cos^2(x) etc.

Okej vad är det jag ska göra? Du glömde att D ska multipliceras med 2. Jag har inga problem med ln^2(y) liknar sin^2(y) men jag stör mig på facit som säger ln(y^2)/2=x^2/2+C

Du räknar nästan rätt, men det går fel här:

Multiplicera med 2 på båda sidor innan du tar roten-ur

Trinity2 skrev:

Du räknar nästan rätt, men det går fel här:

 

Multiplicera med 2 på båda sidor innan du tar roten-ur

Ok

Trinity2 skrev:

Du räknar nästan rätt, men det går fel här:

 

Multiplicera med 2 på båda sidor innan du tar roten-ur

Tack!