Bestäm Z1 och Z2

I del 1: p =2 och q = 3
I del 2: p = a och q = (b-a)/2
Del 3: Hur ska jag tänka? Vi inte riktigt vad som menas med frågan eller hur jag kan gå tillväga för att lösa den.
Hade varit tacksam för lite hjälp. Tack på förhand!
Jag tycker frågan är litet oklar. I del 3, menar de z1 och z2 från del 1?
I så fall kan varje z skrivas som en linjärkombination av z1 och z2, vilket du visat i 2.
Men om z1 = 3+5i och z2 = 30+50i, hur blir det då?
Vad menas med linjärkombination? Och hur kom du fram/såg du detta?
Du får gogla linjärkombination, det ligger kanske inte i gymnasiekursen.
Om du har två riktningar och kan röra dig godtyckligt långt längs dem, så kan du nå vilken punkt som helst i planet (i rymden behöver du tre riktningar). Detta sysslar man mycket med i kursen Linjär algebra, så jag såg svaret nästan innan jag hade läst färdigt frågan.
Men har du två pilar åt samma håll så hjälper det inte hur mycket av den ena du lägger till den andra, totalriktningen blir likafullt samma.
Juste jag minns denna fråga på km. Jag tyckte inte om svaret som stod i facit då det var rätt informellt, gick för mycket på intuition. Jag klagade och då de lade till min lösning, som inte var särskilt bra heller...
Detta är egentligen en fråga som handlar om linjär algebra
Vi har tänkt oss komplexa tal som punkter i det komplexa talplanet. Ett annat sätt är som vektorer från origo:
Om och blir det då såhär:
När man multiplicerar ett komplext tal med någonting kan vi tänka oss att det blir en skalning av denna vektor.
, vilket bara är en längre vektor som , i samma riktning.
Addition av komplexa tal blir då som vektoraddition: 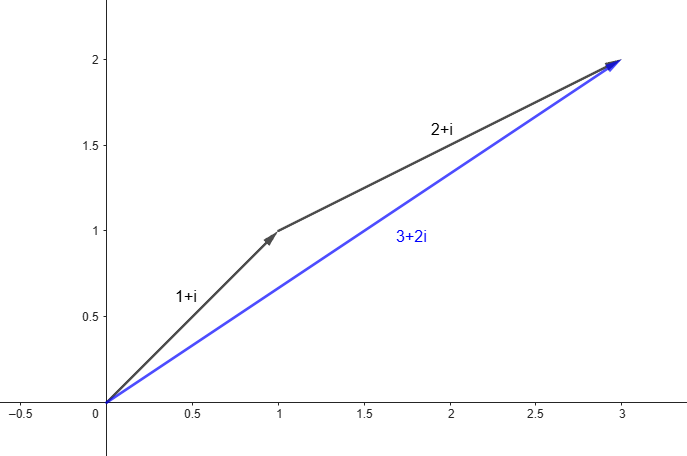
För de flesta val på och kan man kombinera ihop dem för att få vilket tal som helst genom addition och skalning.
Men ibland är det omöjligt att få alla tal. Frågan är när?

