Bestämma c mha rotationen av phi
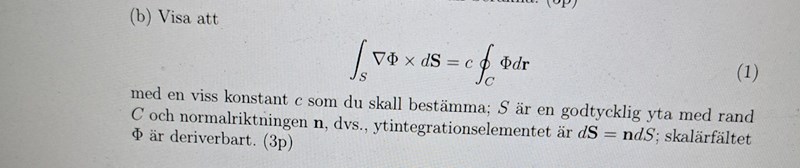
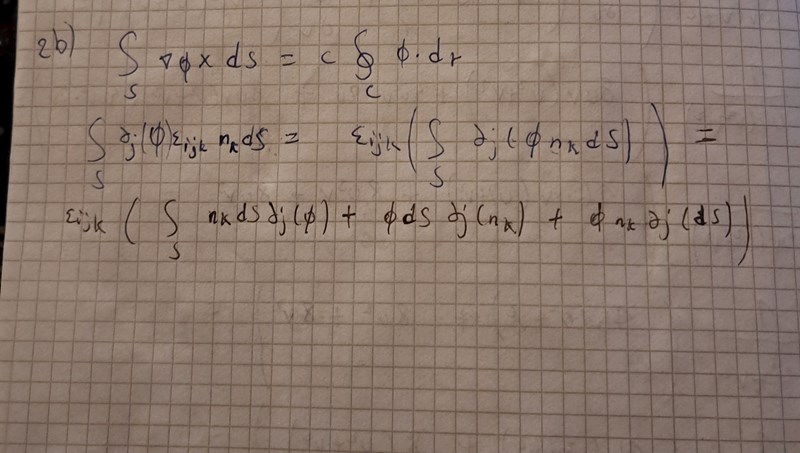
Såhär långt kom jag , men har kört fast på vägen. Jag är osäker på om man ska inte ha fritt index ibörjan dvs sätta Ds till Dsi om resultatet skall bli phi*dr
verkar bara på det skalära fältet . Du ska alltså inte använda produktregeln på
I den här uppgiften ska du visa att en ytintegral (över ytan ) är samma sak som en linjeintegral utmed den slutna kurvan . Det enklaste är att använda en variant av Stokes sats.
Eftersom du räknar med index kan det vara bekvämt att använda någon känd vektorfunktional, till exempel . På indexform blir det
Och då kan du skriva om din integral som
Och alltså är
Jag har ju inte tillgång till er lärobok och ni använder förmodligen en annan notation och lite andra samband, till exempel föredrar jag beteckningen framför , men hoppas du förstår poängen ändå. Annars får du lägga in ett utdrag på den variant av Stokes du vill använda så kanske vi kan lösa den med de skrivsätt ni använder i kursen.
D4NIEL skrev:verkar bara på det skalära fältet . Du ska alltså inte använda produktregeln på
I den här uppgiften ska du visa att en ytintegral (över ytan ) är samma sak som en linjeintegral utmed den slutna kurvan . Det enklaste är att använda en variant av Stokes sats.
Eftersom du räknar med index kan det vara bekvämt att använda någon känd vektorfunktional, till exempel . På indexform blir det
Och då kan du skriva om din integral som
Och alltså är
Jag har ju inte tillgång till er lärobok och ni använder förmodligen en annan notation och lite andra samband, till exempel föredrar jag beteckningen framför , men hoppas du förstår poängen ändå. Annars får du lägga in ett utdrag på den variant av Stokes du vill använda så kanske vi kan lösa den med de skrivsätt ni använder i kursen.
Ok så det bör vara dj eijkphidSk istället nkDs? Vi använder boken ramgard.
Din första ansats är helt korrekt, dvs
är
Men sen verkar du göra någon sorts distribution av deriveringsoperatorn, typ en produktregel.
Det enda fält verkar på är det skalära fältet . Om du vill kan du skriva det som eller
Nästa steg är att leta upp en variant av Stokes sats i indexform i er litteratur eller i er formelsamling.
Det du skrivit är ju samma sak som
D4NIEL skrev:Din första ansats är helt korrekt, dvs
är
Men sen verkar du göra någon sorts distribution av deriveringsoperatorn, typ en produktregel.
Det enda fält verkar på är det skalära fältet . Om du vill kan du skriva det som eller
Nästa steg är att leta upp en variant av Stokes sats i indexform i er litteratur eller i er formelsamling.
Det du skrivit är ju samma sak som
Ok nu har jag detta istället efter korrigering. I formelsamling står det såhär
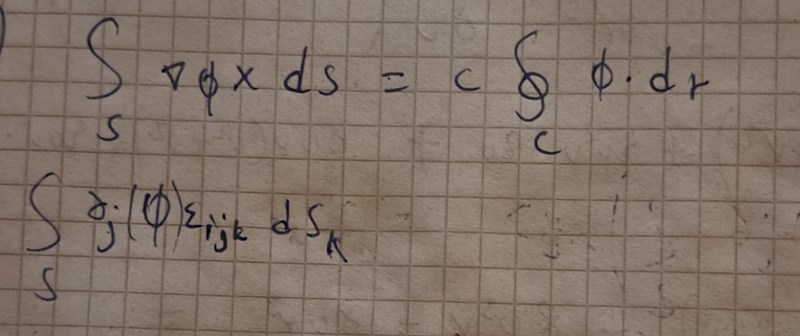

Jättebra, kommer du vidare? Om det känns krångligt kan du tillfälligt byta namn på till .
Då är din integral
Ser du att det blir så? Kan du para ihop det med Stokes sats? Nu är det viktigt att indexen står i rätt ordning, kanske måste man byta ordning på
D4NIEL skrev:Jättebra, kommer du vidare? Om det känns krångligt kan du tillfälligt byta namn på till .
Då är din integral
Ser du att det blir så? Kan du para ihop det med Stokes sats? Nu är det viktigt att indexen står i rätt ordning, kanske måste man byta ordning på
Hur menar du med att byta ordning på index? Såhär långt kom jag och vet bara inte hur man får Ajk i täljaren på högerledet?
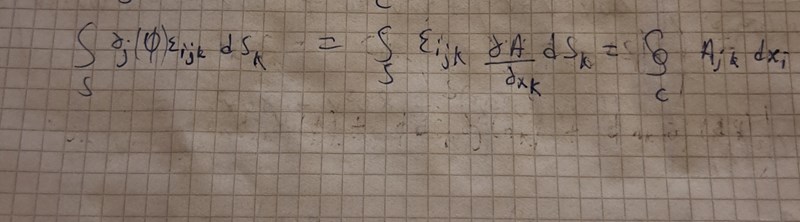
Nu har du ett fritt index längst till vänster och två fria index, , till höger om det första likhetstecknet. Så får man inte göra.
Dessutom är det man deriverar med avseende på.

Korrekt är
Det är alltså viktigt att du deriverar med avseende på inte samt att du ser till att det är samma fria index på båda sidor om ett likhetstecken.
Tensor kan ha ett valfritt antal fria index, inklusive inga index alls i den variant av Stokes sats som du visade ovan.
Om du tittar noga på indexplaceringarna ser du att vi nästan, men inte helt, har det som står i Stokes sats. Man måste genomföra ytterligare en manipulation för att det ska motsvara Stokes sats som den står angiven i #5
D4NIEL skrev:Nu har du ett fritt index längst till vänster och två fria index, , till höger om det första likhetstecknet. Så får man inte göra.
Dessutom är det man deriverar med avseende på.
Korrekt är
Det är alltså viktigt att du deriverar med avseende på inte samt att du ser till att det är samma fria index på båda sidor om ett likhetstecken.
Tensor kan ha ett valfritt antal fria index, inklusive inga index alls i den variant av Stokes sats som du visade ovan.
Om du tittar noga på indexplaceringarna ser du att vi nästan, men inte helt, har det som står i Stokes sats. Man måste genomföra ytterligare en manipulation för att det ska motsvara Stokes sats som den står angiven i #5
Okej jag hänger inte med riktigt på varför det ska vara xj och inte xk?
betyder "derivata med avseende på koordinat, så
Är du med?
Dessutom är det bra om du alltid kontrollerar grundläggande räkneregel för att det inte ska bli fel. Till exempel
- Ett index får förekomma högst två gånger, ett index som förekommer två gånger kontraheras
- Det ska vara samma fria index på båda sidor om ett likhetstecken
Det här termen har till exempel tre förekomster av och kan därmed omöjligt vara korrekt.
 Dessutom har den två fria index, , vilket inte stämmer med att vänstersidan bara har ett fritt index . Om du kontrollerar och följer de enkla reglerna är det enkelt att hitta slarvfel.
Dessutom har den två fria index, , vilket inte stämmer med att vänstersidan bara har ett fritt index . Om du kontrollerar och följer de enkla reglerna är det enkelt att hitta slarvfel.
Test
betyder "derivata med avseende på koordinat , så
Happ, Latex är trasigt i tråden
D4NIEL skrev:betyder "derivata med avseende på koordinat, så
Är du med?
Dessutom är det bra om du alltid kontrollerar grundläggande räkneregel för att det inte ska bli fel. Till exempel
- Ett index får förekomma högst två gånger, ett index som förekommer två gånger kontraheras
- Det ska vara samma fria index på båda sidor om ett likhetstecken
Det här termen har till exempel tre förekomster av och kan därmed omöjligt vara korrekt.
Dessutom har den två fria index, , vilket inte stämmer med att vänstersidan bara har ett fritt index . Om du kontrollerar och följer de enkla reglerna är det enkelt att hitta slarvfel.
Yes men då ska det vara eijkdA/dxjSk för då är i fritt, j förekommer två gånger och samma sak med k.
Vad blir nästa steg nu?
Jämför med din formel i #5. Vilket index är fritt i deras formel (1,2 eller 3)? Vilket index deriverar de med avseende på?
Hur ska du manipulera ditt uttryck för att få samma uttryck som de har?
D4NIEL skrev:Jämför med din formel i #5. Vilket index är fritt i deras formel (1,2 eller 3)? Vilket index deriverar de med avseende på?
Hur ska du manipulera ditt uttryck för att få samma uttryck som de har?
Index som är fritt är ju i hela tiden på båda leden. Det blir ju som du sa liksom. Jag deriverar map på xj
Jag vet inte vad du menar med manipulera uttryck för att få samma svar som de har?

är ett fritt index och det står på plats 1 i
förekommer två gånger, det står på plats 2 i och det är det index man använder i
förekommer två gånger, det står på plats 3 i och det är det index som sitter på derivatan.
I ditt uttryck måste du alltså flytta runt indexen så att du har det index som deriverar på plats 3 och det index som sitter på på plats 2.
Ett enkelt sätt att göra det är att byta plats på och , och då byter tecken.
D4NIEL skrev:
är ett fritt index och det står på plats 1 i
förekommer två gånger, det står på plats 2 i och det är det index man använder i
förekommer två gånger, det står på plats 3 i och det är det index som sitter på derivatan.
I ditt uttryck måste du alltså flytta runt indexen så att du har det index som deriverar på plats 3 och det index som sitter på på plats 2.
Ett enkelt sätt att göra det är att byta plats på och , och då byter tecken.
Ja då blir -eikjdA/dxjdSk. Jag antar det är minus pga eijk=-eikj. Vad händer sen?
Sen kan du byta ut det mot linjeintegralen rakt av från formelsamlingen (Stokes sats), byta tillbaka från till och så är det klart.
D4NIEL skrev:Sen kan du byta ut det mot linjeintegralen rakt av från formelsamlingen (Stokes sats), byta tillbaka från till och så är det klart.
Vad är dxi?
Det är linjeelementet (eller mer egentligt lägesvektorns differential) . I kartesiska koordinater motsvarar det
I sfäriska koordinater blir det istället
D4NIEL skrev:Det är linjeelementet (eller mer egentligt lägesvektorns differential) . I kartesiska koordinater motsvarar det
I sfäriska koordinater blir det istället
Ja ok. Jaha juste i formelsamlingen har vi ju dxr som då är lika med dxi i mitt fall.
Ja just det. Notera att det blir det fria indexet som ska sitta på dx så att du får samma fria index på båda sidor om likhetstecknet.
Kontrollera alltid att du har rätt antal fria index på båda sidor och att de heter samma sak. Om det inte stämmer vet du att det har blivit ett slarvfel någonstans :)
D4NIEL skrev:Ja just det. Notera att det blir det fria indexet som ska sitta på dx så att du får samma fria index på båda sidor om likhetstecknet.
Kontrollera alltid att du har rätt antal fria index på båda sidor och att de heter samma sak. Om det inte stämmer vet du att det har blivit ett slarvfel någonstans :)
Ska ha detta i åtanke. Tack!

