Bestämma egenvektor med egenvärde.

håller på med den här uppgiften:

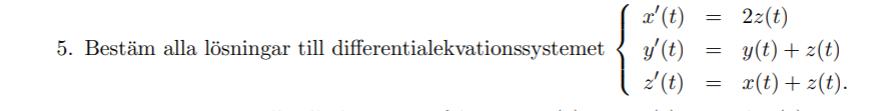
Har fått ut egenvärden: $λ = 1, λ = - 1, γ = 2$
Men jag förstår inte riktigt hur man bestämmer egenvektorer.

för $λ = 1 : \begin{matrix} - 1 & 0 & 2 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}$ så är egenvektorn $s \begin{matrix} 0 \\ 1 \\ 0 \end{matrix}$

och jag förstår inte hur man avgör det.
Jag kan se att $- x + 2 z = 0 \leftrightarrow x = 2 z x = 0 z = 0$

och för att vi kan på något sett bekräfta att x och z är 0 men inte y så sätter vi sätter vi y som 1?

Men jag kan inte använda samma logik för andra egenvektorer. Kan någon förklara exakt hur det funkar när man bestämmer egenvektor med olika egenvärden. Kan någon visa hur man kom fram till egenvektorn $\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}$ ?

Din matris du har är matrisen

(A-cE), där A är din ursprungliga matris, c är egenvärdet och E identitetsmatrisen.

För att hitta egenvektorer, X, till egenvärdet c, så ska du lösa

(A-cE)X=0.

Så om du Gaussar din matris, bör du få minst en nollrad (fundera på varför), alltså en parameterlösning.

Din matris kan reduceras till

[1 0 0

0 0 1

0 0 0]

Vilket ger lösningen

x=0, y=t (parameter), z=0

eller på vektorformen

t(0 1 0)^T

jamolettin skrev:
Din matris du har är matrisen

(A-cE), där A är din ursprungliga matris, c är egenvärdet och E identitetsmatrisen.

För att hitta egenvektorer, X, till egenvärdet c, så ska du lösa

(A-cE)X=0.

Så om du Gaussar din matris, bör du få minst en nollrad (fundera på varför), alltså en parameterlösning.

Din matris kan reduceras till

[1 0 0

0 0 1

0 0 0]

Vilket ger lösningen

x=0, y=t (parameter), z=0

eller på vektorformen

t(0 1 0)^T

tack för hjälpen, jag förstår hur man tänker nu! :)

Svara