Bestämma ekvation ifrån graf
Hej, jag skulle behöva hjälp med denna uppgift. Som jag förstår det måste jag först få ut vad det är dör ekvation på kurvan innan jag räknar ut tangentens ekvation. Men jag vet inte hur jag genom grafen får ut en ekvation.
uppgift: Bestäm riktningskoefficienten till tangenten i punkten där x=-2
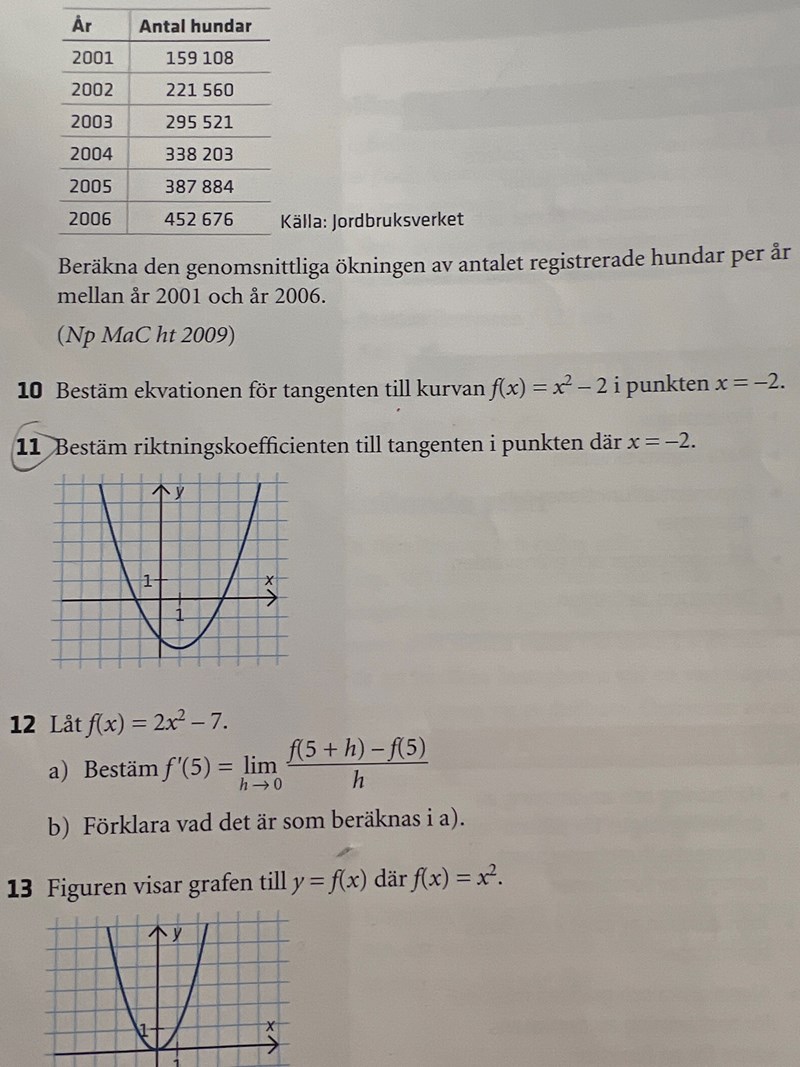
Ta några punkter som ser väldefinierade ut, t.ex. (2, -2) och (4, 2). Tillsammans med symmetriaxeln x = 1 kan du få fram funktionen.
Jag vet det där men vet int vad jag ska göra med punkterna
Någon sådan uppgift borde du ha fått lösa innan den här kom.
Ställ upp en generell formel för en andragradsekvation (det står inte att det är det, men det ser ut som det) och sätt in det du vet så kan du bestämma alla koefficienter.
Men jag börjar misstänka att du bara ska lösa uppgiften grafiskt. Ta en linjal och lägg den som den nämna tangenten. Ta reda på lutningen.
I den här boken 3c har jag ej löst liknade, jag har gjort det i förra boken 2c då vi jobbade med andragradsekvationer och skulle då endast ta reda på grafens ekvation, så jag har glömt bort lite hur man gör. Kan du visa hur du menar med att ställa upp en generell formel?
även om jag nu endast ska använda linjal till denna uppgift är det bra att jag lär mig utan linjal till framtiden om det kommer liknade uppgifter
Det är nog ännu bättre att du lär dig metoden MED linjalen!
Eftersom vi vet att x = 1 är symmetriaxeln så skulle jag ställa upp y = a(x-1)2 + b. (Annars kan man ta ax2+bx+c.)
Sätter jag in punkterna får jag
-2 = a + b
2 = 9a + b
Jo, visst. Men metoden med linjalen kan jag men jag trodde att man skulle räkna ut det, då man ofta ska räkna ut exakta värden och om jag mäter med linjalen blir det ju troligen en felkälla att jag (hur mkt jag en försöker) mäter inte exakt
Det blir inte exakt hur du än gör.
För att den algebraiska metoden ska bli exakt måste du dels veta vilken typ av funktion som grafen motsvarar (andragradsfunktion?), dels veta att koordinaterna du väljer faktiskt ligger på kurvan.
Du kan inte med säkerhet veta något av detta, även om det verkar vara så.
Men det är helt OK att i början av en algebraisk lösning ange dessa antaganden som förutsättningar.




