bestämma funktion ut av grafen

Du kan tänka på de asymptoter, som uppenbart finns i grafen.

Jag är med på att jag måste ta hänsyn till asymptoterna men hur tar jag mig därifrån. Ja har inget minne av att jag har sett en liknande funktion.

Har du bestämt en funktion för någon enklare graf med asymptoter?

 Andra och tredje gradare samt (x+y)^2-(x-y)^2=1 är några exempel på funktioner som jag bestämt utifrån graf

Inga asymptoter? Då tycker jag den här uppgiften är lite svår för att vara den första med asymptoter. Kan du komma på en enkel funktion som har både vertikala och horisontella asymptoter (en eller flera)? Den kan man bygga vidare på sedan.

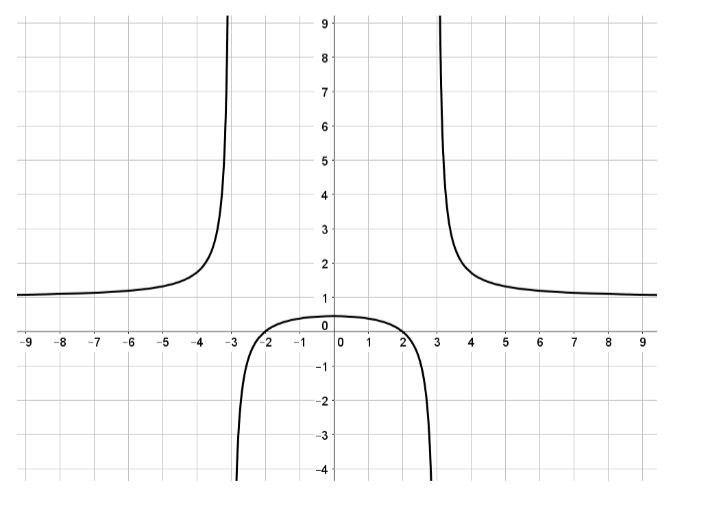
När nämnaren är noll ger det de typiska lodräta asymptoterna du ser vid $x=-3$ och $x=3$. Du kan alltså konstatera att nämnaren kommer att ha nollställena $x=-3$ och $x=3$.

Du ser även att funktionen skär $y$-axeln vid $x=-2$ och $x=2$. Detta hjälper dig att bestämma täljaren.

Vad är det för typ av funktioner som har en lodrät asymptot?

Jag gjorde en gissning att funktionen var $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ men den ska förskjutas och tryckas ihop lite. För att förskjuta den y led så lägger kan jag lägga till en konstant men för att trycka ihop den

boman98 skrev:

Jag gjorde en gissning att funktionen var $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ men den ska förskjutas och tryckas ihop lite. För att förskjuta den y led så lägger kan jag lägga till en konstant men för att trycka ihop den

 Nja, detta blir väldigt krångligt. Försök istället att göra det med ett bråkstreck.

Du visste att nämnaren skulle ha nollställena $x=-3$ och $x=3$. Detta ger att uttrycket i nämnaren bör vara $(x+3)(x-3)=x^2-9$.

Så nämnaren innehåller något med x+3 och x-3 och täljaren något med x+2 och x-2.

Kan någon förklara varför det den ska bli$\frac{x^2-4}{x^2-9}$

AlvinB skrev:

boman98 skrev:

Jag gjorde en gissning att funktionen var $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ men den ska förskjutas och tryckas ihop lite. För att förskjuta den y led så lägger kan jag lägga till en konstant men för att trycka ihop den

 Nja, detta blir väldigt krångligt. Försök istället att göra det med ett bråkstreck.

Du visste att nämnaren skulle ha nollställena $x=-3$ och $x=3$. Detta ger att uttrycket i nämnaren bör vara $(x+3)(x-3)=x^2-9$.

 $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ har ju faktiskt formen  $a + \frac{b}{x^2-9}$, bara med fel konstanter.

Laguna skrev:

AlvinB skrev:

Visa föregående citat

boman98 skrev:

Jag gjorde en gissning att funktionen var $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ men den ska förskjutas och tryckas ihop lite. För att förskjuta den y led så lägger kan jag lägga till en konstant men för att trycka ihop den

 Nja, detta blir väldigt krångligt. Försök istället att göra det med ett bråkstreck.

Du visste att nämnaren skulle ha nollställena $x=-3$ och $x=3$. Detta ger att uttrycket i nämnaren bör vara $(x+3)(x-3)=x^2-9$.

 $\frac{x-3}{x+3}+\frac{x+3}{x-3}$ har ju faktiskt formen  $a + \frac{b}{x^2-9}$, bara med fel konstanter.

 Jo, jag vet, men det är mycket krångligare att sedan hålla på och bestämma täljaren. Om man skriver allt med ett bråkstreck faller svaret ut nästan direkt.

boman98 skrev:

Kan någon förklara varför det den ska bli$\frac{x^2-4}{x^2-9}$

 Om ett bråk skall ha värdet 0, krävs det att täljaren är 0. Du vill ha ett bråk som har värdet 0 när x = 2 och när x =-2. Då behöver täljaren vara ett uttryck som hr värdet 0 när x = 2 och när x =-2, men inte annars.

Hej!

En rationell funktion $f(x) = t(x)/n(x)$ som har nollställen $x=-2$ och $x=2$ och inga fler har täljarfunktionen $t(x)$ som är ett andragradspolynom $(x-2)(x+2) = x^2-4$.

Nämnarpolynomet ska ha nollställen $x=-3$ och $x=3$ och inga fler, vilket betyder att $n(x) = (x-3)(x+3) = x^2-9$.

Den rationella funktionen $f(x) = (x^2-4)/(x^2-9)$ har en graf som ser ut såhär.

Hej Benjamin.

Jag antar att du är bekant med gränsvärden och rationella funktioner?

Om bilden visar grafen till den rationella funktionen $f(x)$ så verkar det som att

• funktionens nollställen ligger vid $x=\pm 2$.
• funktionen värde vid $x=0$ är i närheten av 0,5.

• gränsvärde saknas då x går mot plus (och minus) 3, dvs här finns vertikala asymptoter.
• gränsvärdet då x går mot positiva (och negativa) oändligheten är ungefär lika med 1, dvs här finns en horisontell asymptot.

Det betyder (enligt resonemang från tidigare svar) att $f(x)$ kan skrivas på formen $f(x)=k\cdot \frac{x^2-4}{x^2-9}$, där $k$ är en konstant som ligger ganska nära 1.

Pröva gärna i Desmos med olika värden på $k$.