Bestämma gränserna för en dubbelintegral
Hej!
Jag läste flervariabelanalys förra året och har därför behövt repetera hur man dubbelintegrerar i första laget. Nu tror jag att jag minns. Jag sitter däremot med detta område:
och jag kan inte komma på vad för integrationsgränser jag ska ha. Jag ritade upp området och verfierade med Desmos:
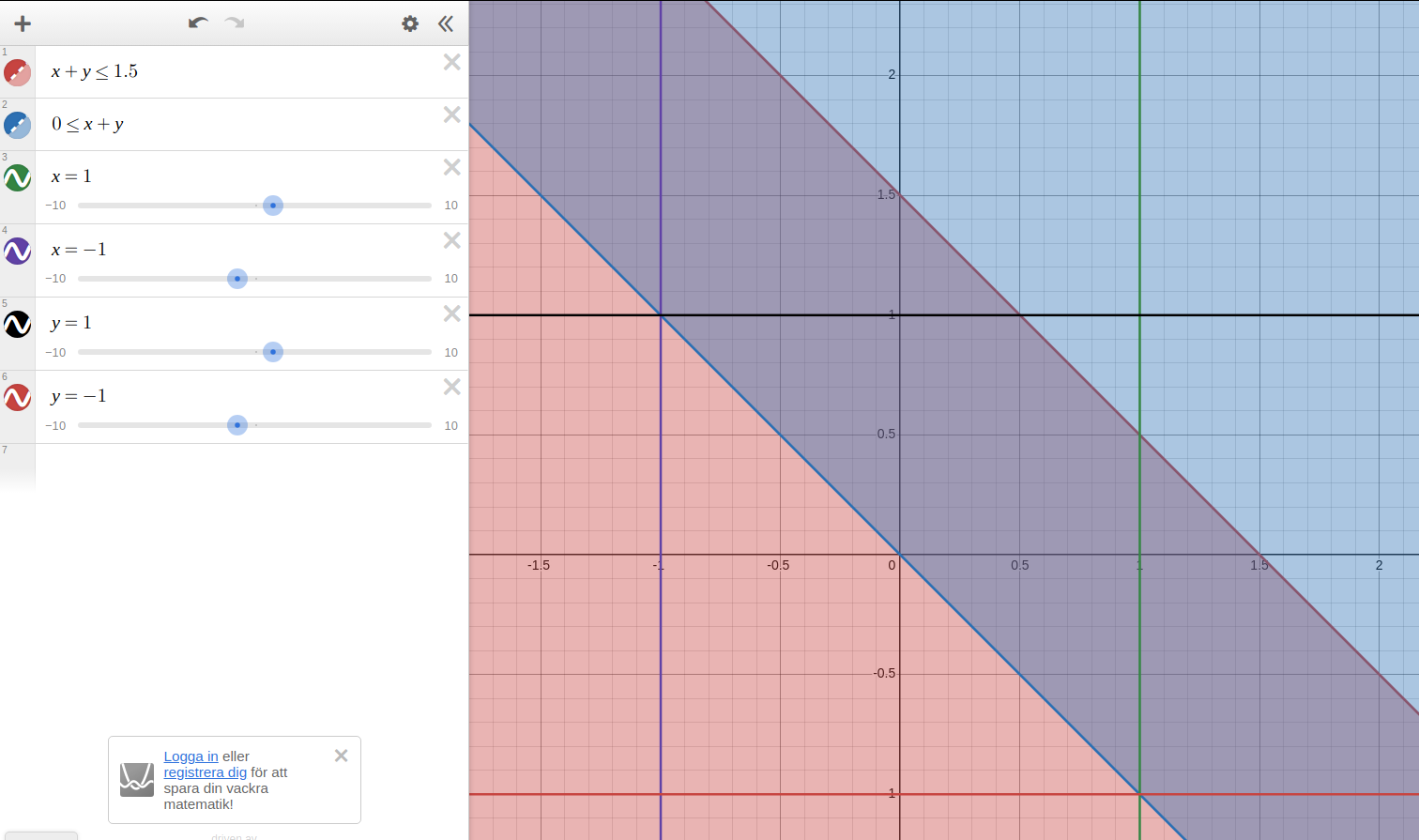
Jag tänker mig att man först måste integrera upp till (i x-led), men sedan skär denna linje , och där måste man använda som övre gränsen för dubbelintegralen. (skärningen sker i
Alltså tänker jag mig detta (tänker att det är gränserna som är det viktiga, därav inkluderar jag inte funktionen för tillfället):
Men det verkar ha blivit lite tokigt. Var har jag gjort ett misstag?
Det ser ok ut. Jag hade nog valt x som yttre integral men det är en smaksak.
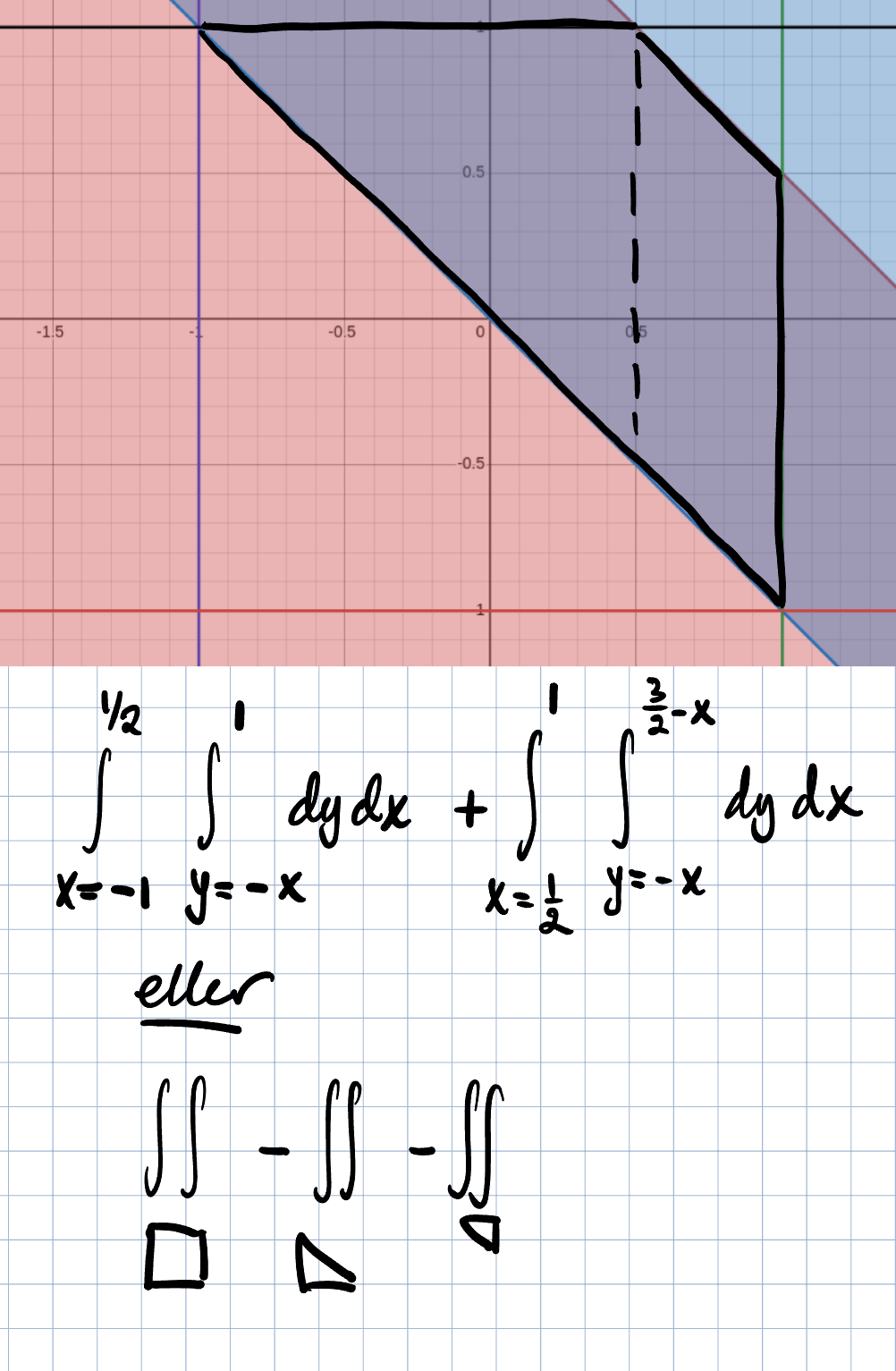
Jag hade svårt att tolka din figur såp jag ritade en egen. Ska se vart det leder. Återkommer.

Så här blev det för mig. Du verkar vara inne på ungefär samma spår, du får jämföra. Nej, jag ser att Trinity2 har varit inne också.
För egen del föredrar jag att rita för hand. Det blir inte lika snyggt, men jag tycker man lär sig mer på det.

Tack för hjälpen hörni! Jag trodde att jag hade fått fram fel gränser, men testade igen - ny dag nya tag. Med den triviala integralen över området som beskrivs av olikheterna i OP så får jag samma area som olikheten beskriver.
Marilyn:
För egen del föredrar jag att rita för hand. Det blir inte lika snyggt, men jag tycker man lär sig mer på det.
Jag med! Jag ritade upp allt på papper först. Bilden från Desmos var för tydlighetens skull (och för att jag matade in olikheterna där efter att jag tänkt på papper:))

