Bestämma kraftens moment för bult

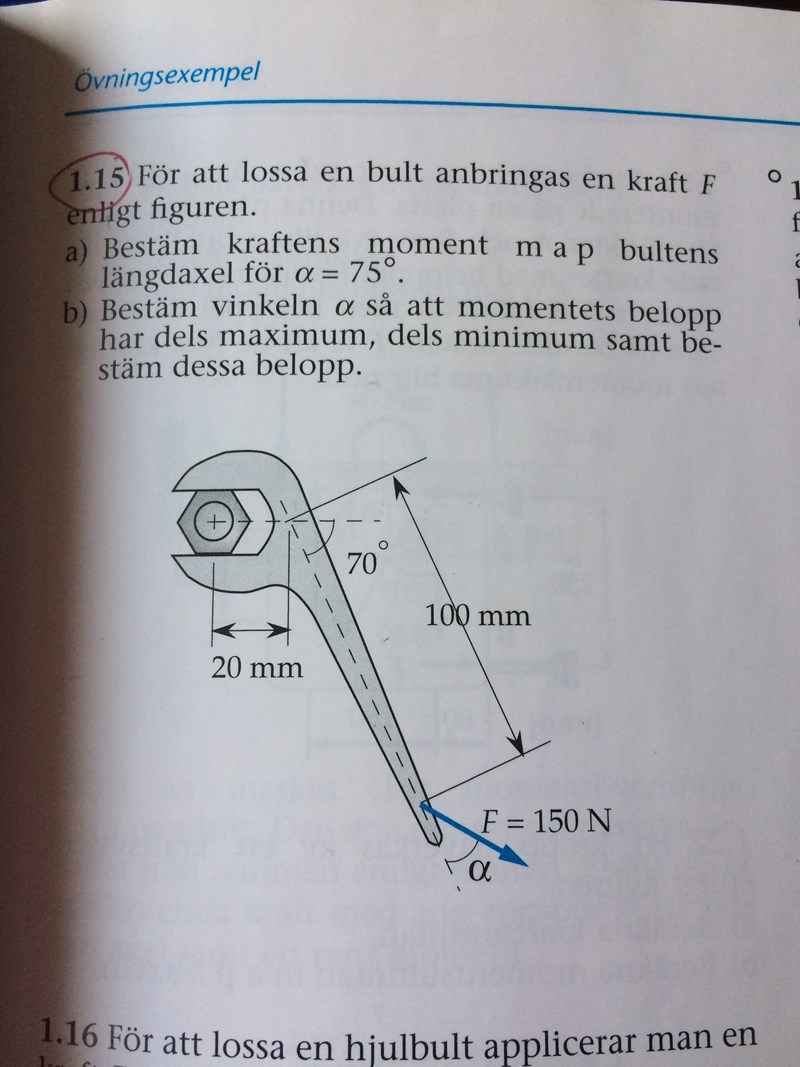
Jag har fastnat på fråga a. Enligt det lösningsförslag vi fått av vår lärare ska:

$f_{x} = F \times \cos (α + 20) f_{y} = F \times \sin (α + 20)$

Men jag förstår inte varför man lägger på 20 grader? Hur skulle ni löst uppgiften?

Om x-axeln är den "normala", dvs pekar åt höger i bild har din lärare slarvat ihop x- med y komposanten.

Orsaken till (+20°) är att skiftnyckeln lutar 20 grader mot vertikalen (y-axeln)

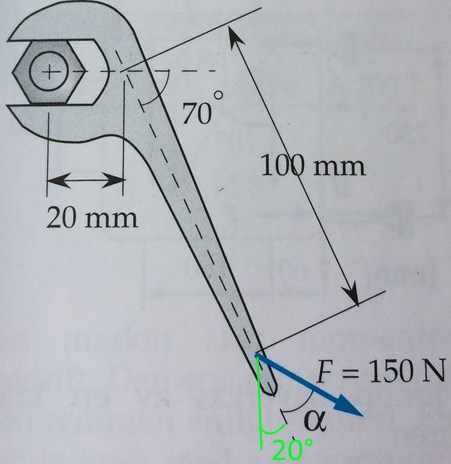Så här skulle jag löst a) uppgiften:

$\vec{r}\times\vec{F}=(0.02\angle 0^{\circ}+0.1\angle -70^{\circ})\times(150\angle 5^{\circ})\approx 14.8\mathrm{Nm}$

Jroth skrev:
Om x-axeln är den "normala", dvs pekar åt höger i bild har din lärare slarvat ihop x- med y komposanten.
Orsaken till (+20°) är att skiftnyckeln lutar 20 grader mot vertikalen (y-axeln)
Så här skulle jag löst a) uppgiften:
$\vec{r}\times\vec{F}=(0.02\angle 0^{\circ}+0.1\angle -70^{\circ})\times(150\angle 5^{\circ})\approx 14.8\mathrm{Nm}$ "

Tack. Hade du kunnat förklara hur man kommer fram till att skiftnyckelnlutar 20 grader mot y-axeln? Går detta att beräkna på något sätt eller ska man "bara se det"?

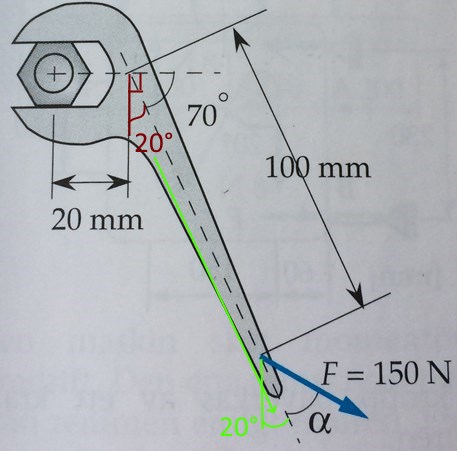
Man kan "enkelt" se det eftersom skiftnyckeln lutar 70° mot x-axeln (se markering överst i bild).

Vinkeln mellan x-axeln och y-axeln måste vara 90°.

Skiftnyckeln, dvs den streckade linjen, lutar alltså 90°-70°= 20° mot y-axeln. Se röd markering. Detta är samma vinkel som skiftnyckeln (den streckade linjen) fortfarande bildar med y-axeln nere till höger (den gröna markeringen).

Är du med?

Svara

Visa senaste svar