9 svar

515 visningar

skrållan100 behöver inte mer hjälp

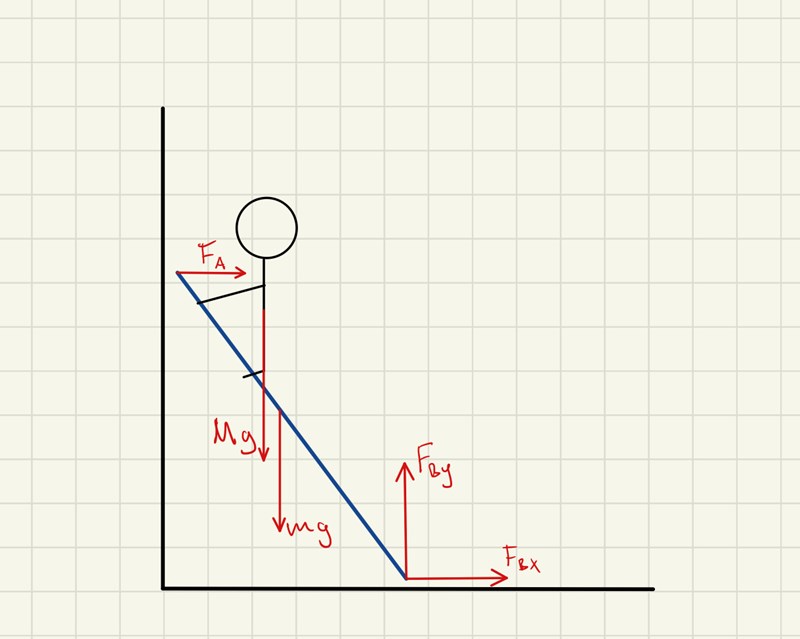
Bestämma krafter på stege

Hej,

jag försöker lösa denna uppgift:

Såhär tänkte jag:

Krafter som vrider medurs: $F_{g, g u b b e}, F_{g, s t e g e}$

Systemet är i jämvikt om momentet = 0.

Räknar ut avstånd från B till stegens mitt genom att först räkna ut stegens totala längd (via Pyth. sats) och dela på två. $L = 3, 2 m$

Räknar ut avståndet från B till gubben genom att
1) Räkna ut vinkeln mellan vägg och stege vid A. Uträkning ger: $α = 18 °$
2) Skapa en liten triangel med vinkeln, en sida på 0,8 m och hypotenusan (som motsvarar sökt längd)
Uträkning ger: $L = 3, 9 m$

$\underset{M}{\to} = 3, 9 * F_{g, g u b b e} + 3, 2 * F_{g, s t e g e} = 3, 9 * 70 * 9, 82 + 3, 2 * 10 * 9, 82 = 2995, 1 N m$

För att jämvikt ska uppnås ska momentet moturs vara lika stort som momentet medurs. Om B är vridningspunkten kommer det ej vara moment här, dvs:

$\underset{M}{\leftarrow} = 6 * F_{v ä g g} \frac{2995, 1}{6} = F_{v ä g g} F_{v ä g g} = 499 N$

Krafterna medurs och moturs ska även tillsammans vara lika med noll:
$F_{g, t o t} = F_{g, g u b b e} + F_{g, s t e g e} = 785 N F_{g, t o t} = F_{v ä g g} + F_{g o l v} F_{g o l v} = F_{g, t o t} - F_{v ä g g} = 785 - 499 = 285 N$

Alltså får jag att:
- Krafter som verkar i A = 499N

- Krafter som verkar i B = 285 N

Detta är fel, hur ska jag tänka?

Du räknar ut momentet moturs med längden 6 m, vilket är rätt, men medurs borde du använda det horisontella avståndet från B, inte längden upp längs stegen.

Okej, då gjorde jag såhär nu:

Tänkte att det totala momentet ska vara noll. Då fick jag:

Sträcka stege:
$l^{2} = 6^{2} + 2^{2} l = 6, 3 m$

A)
$M_{A} = (m_{g u b b e} g * 0, 8) + (m_{s t e g e} g * 0, 5 * 6, 3) - F_{A} * 0 - F_{B} * 2 = 0 \Rightarrow 859, 25 - 2 F_{B} = 0 \Rightarrow F_{B} = 429 N$

Medsols.

B)
$(m_{g u b b e} g * 1, 2) + (m_{s t e g e} g * 6, 3 * 0, 5) - F_{A} * 2 - F_{B} * 0 = 0 1134, 21 = 2 F_{A} F_{A} = 567, 1 N$

Medsols.

Ingen av dessa krafter blir dock rätt. Är det fel att utgå från att systemet ska vara lika med noll? Eller är det andra längder jag ska använda?

M = m_gubbe. m = m_stege.

Mg $\cdot$ 0,8 + mg $\cdot$ 1,0 - $F_{B y} \cdot 2, 0 - F_{B x} \cdot 6, 0$ = 0

Mg $\cdot$ 1,2 +mg $\cdot$ 1,0 - F_A $\cdot$ 6,0 = 0

Tack!

Efter jag ställer upp moment-ekvationerna får jag:

Utgår från B: $F_{A} = \frac{1}{6} (m_{1} g * 1, 2 + m_{2} g) = 153, 8 N$

Utgår från A: $2 F_{B y} + 6 F_{B x} = m_{1} g * 0, 8 + m_{2} g * 1 F_{B y} + 3 F_{B x} = 324, 06 N$

Sen tänkte jag summera krafterna för att kunna ta reda på de okända värdena

$\sum_{}^{} F_{x} = F_{A} - F_{B x} \sum_{}^{} F_{y} = m_{1} g + m_{2} g - F_{B y}$

Den första summeringen ger genom insättning $F_{A} = F_{B x} = 153, 8 N$

Från tidigare momentekvation (utgång fr A) ges: $F_{B y} = 324, 06 - 3 F_{B x} = 324, 06 - 461, 4 = - 137, 5 N$

DVS, SVAR:
$F_{B y} = - 137, 5 N F_{B x} = 153, 8 N F_{A} = 153, 8 N$

Det stämmer att två krafter ska vara lika stora. Alla värden är dock fel, är det fel sätt att summera?

Vad säger facit?

Hursomhelst är ett negativt svar på F_By inte rimligt.

Facit säger:

$N_{A} = 154 N N_{B} = 785 N N_{c} = 154 N$

Kan inte ett negativt svar betyda att kraften är felriktad i ritningen?

Låt oss sätta upp ekvationerna och se vad vi får.

Moment kring punkten B:

6F_A - 1,2Mg - 1,0mg = 0,

vilket ger F_A = (1,2M + 1,0m)g/6 = (1,2*70+1,0*10)*9,82/6 = 153,84 N $\approx$ 1,5 x 10² N.

Kraftjämvikt i horisontalled:

F_A + F_B_x = 0,

vilket ger F_Bx = -F_A $\approx$ -1,5 x 10² N. Dvs F_Bx är riktad till vänster, och inte åt höger som jag ritade, vilket faktiskt verkar rimligt när man tänker på det.

Kraftjämvikt i vertikalled:

F_By - Mg - mg = 0,

vilket ger F_By = (M + m)g = 80*9,82 = 785,6 N $\approx$ 7,9 x 10² N.

Så vi får samma svar som facit, som har lite väl många värdesiffror, givet den noggrannhet som vi får värden med i problemet.

Frågor på det?

Nej, men tack så mycket för hjälpen!! :D

Svara

Visa senaste svar