Bestämma masscentrum över resterande kropp


Hej!
Jag har ganska mycket problem med uppgifter som har med masscentrum att göra. Här försökte jag bestämma masscentrum för hela kroppen mha sambandet för sammansatt kropp och började med triangelskiva. I boken finns det redan en härledd masscentrum för triangelskiva och det går inte så bra när jag försöker bestämma masscentrum för likbent triangelskiva. Hur ska jag gå vidare härifrån? Är det bättre att använda sig av den härledda svaret på masscentrum direkt bara från triangelskiva samt halvcirkelskiva för att spara tid?
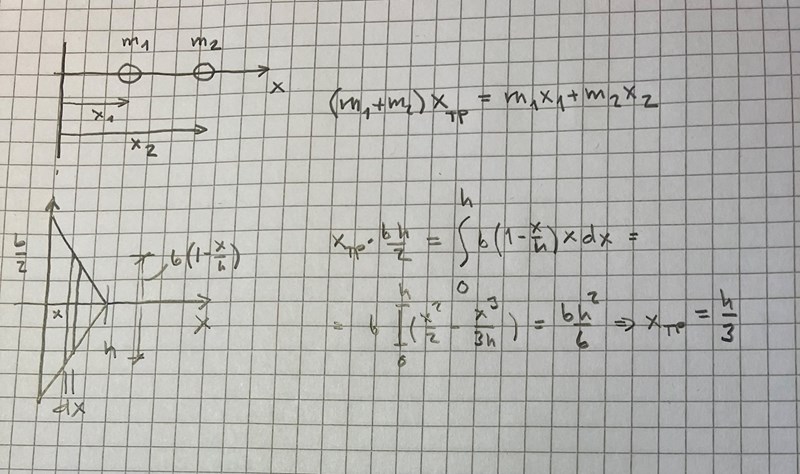
Grunden för TP-bestämningar visas i övre figuren för två massor (eller "ytor med tjocklek").
Tillämpas det på en triangel enligt undre figuren, med basen b och höjden h, svarar det mot att tyngdpunkten xtp gånger hela ytan bh/2 är "summan", integralen av längder x från y-axeln gånger ytor av tunna skivor dx * b(1-x/h), som uträknat ger xtp =h/3. (R/6 i uppgiften)
Sen får man göra samma beräkning för en halvcirkel (lämpligen med r -fi - koordinater och inte x -y) och komma fram till att xtp = 4R/3pi.
Slutligen använda samma resonemang för restytan som för de två massorna i övre figuren.
Var detta till någon hjälp?
När det gäller trianglar finns det en sats om "ekvimomenta system" som säger att tyngdpunkten fås genom att placera en tredjedel av triangelns massa (yta) i vardera av triangelsidornas mittpunkter. Prova och se vilket resultatet blir för triangeln ovan.
hansa skrev:
Grunden för TP-bestämningar visas i övre figuren för två massor (eller "ytor med tjocklek").
Tillämpas det på en triangel enligt undre figuren, med basen b och höjden h, svarar det mot att tyngdpunkten xtp gånger hela ytan bh/2 är "summan", integralen av längder x från y-axeln gånger ytor av tunna skivor dx * b(1-x/h), som uträknat ger xtp =h/3. (R/6 i uppgiften)
Sen får man göra samma beräkning för en halvcirkel (lämpligen med r -fi - koordinater och inte x -y) och komma fram till att xtp = 4R/3pi.
Slutligen använda samma resonemang för restytan som för de två massorna i övre figuren.
Var detta till någon hjälp?
När det gäller trianglar finns det en sats om "ekvimomenta system" som säger att tyngdpunkten fås genom att placera en tredjedel av triangelns massa (yta) i vardera av triangelsidornas mittpunkter. Prova och se vilket resultatet blir för triangeln ovan.
Jag lyckades lösa uppgiften nu.

