Bestämma ström
Behöver hjälp med följande fråga och det är C) jag behöver hjälp med:
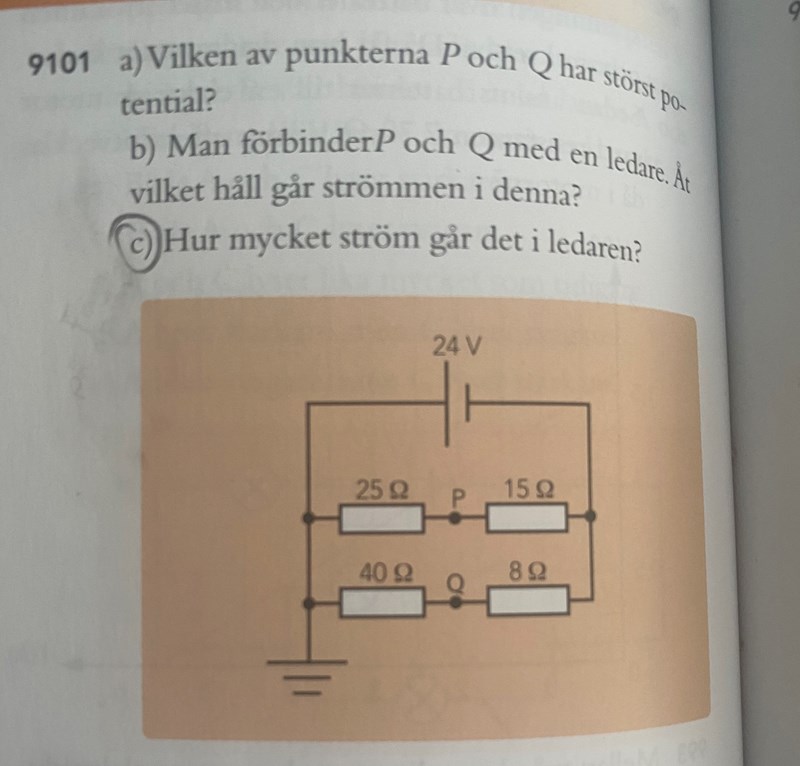Jag är heeeeelt förvirrad och förstår mig inte alls på hur man löser detta trots att jag kollat på lösningsförslagså jag tänkte visa lösningsförslaget och förklara vad jag inte fattar:
mitt första problem är att jag inte begriper varför ledaren gör att punkterna får samma potential och varför detta gör att alla strömmar förändras. Vidare fattar jag inte varför de beräknar den totala strömmen genom att tänka att det är två parallellkopplingar, en till vänster och en till höger, som sedan bildar en seriekoppling av resistorer. Vad är det som gör att det bli fel om jag tänker att det är två seriekoppling, en övre och en under, som sedan bildar en parallellkoppling av resistorer?
Det står även att det gör en ström I1 från 25 motståndet och en annan ström I2 från 15 motståndet, men dessa två motstånd är seriekopplade och i en seriekoppling är ju ström lika överallt?
Till sist har jag problem med att de använder den beräknade totala strömmen i hela kretsen och den beräknade ersättningsresistansen på de vänstra motstånden för att räkna ut spänningen över dessa och på samma sätt använda ersättningsresistansen för de högra parallellkopplade motstånden och strömmen i kretsen för att beräkna spänningen Över dessa. Men i en parallellkoppling är ju strömmen inte lika överallt så ut kan de räkna på det sättet och använda sig av toralströmmen?
Som sagt är jag helt förvirrad och allt verkar fel i mitt huvud när jag läser detta. Jag har prov imorgon och hjälp skulle uppskattas oerhört mycket!
Den elektriska potentialen skiljer sig mellan två punkter om det krävs energi för att flytta sig mellan dessa. ...åtminstone om man är en elektrisk laddning. I en ledare rör sig strömmen mycket lätt (det är därför det går så mycket ström om man kortsluter batteriet), så om kopplar ihop punkter med en elektrisk ledare så får de samma potential, för strömmen kan flytta sig mellan punkterna utan motstånd.
Om du tittar på ditt exempel och ändrar det lite -- ersätt 8-ohms resistorn nere till höger med en ledare så att strömmen kan gå där utan motstånd, ersätt sen också 25 ohms resistorm uppe till vänster med en ledare så att strömmen kan gå där utan motstånd. Känner du då att hela kopplingen (innan man kopplar ihop P och Q) är en parallellkoppling av 15 ohm och 40 ohm? Om man därefter kopplar ihop P och Q, känner du att strömmen kommer att gå genom ledaren uppe till vänster (som ersatte 25 ohms resistorn) och sen från P till Q för att ta den enkla vägen till ledaren som ersatte 8 ohms motståndet nere till höger? Om du själv låtsas att du är en elektron, kan du känna att när du kommer till valet mellan 40 och och 25 ohm (eller ännu bättre inget motstånd alls) att du helst tar vägen uppe till vänster -- och när du sen kommit till P så kan du gå vägen via Q och sen ta den enklare vägen nere till höger. Strömmen (och du som elektron) kommer alltid helst att ta minsta motståndets väg.
Jag tror att om du får en känsla för varför potentialen i två sammankopplade punkter är densamma så kommer resten att falla på plats.
Okej då förstår jag varför det är så och jag förstår även att de beräknar den totala strömmen. Däremot förstår jag fortfarande inte resterande delen av lösningen, bland annat varför de väljer att beräkna ersättningsresistansen över parallellkopplingarna och inte seriekopplingarna, vilket de sedan använder för att beräkna spänningen i 25 motståndet och 15 motståndet. När dessa spänningar beräknas används ju totala strömmen 1.16 men eftersom motstånden är parallellkopplade är ju strömmen olika? Eller får man räkna på den totala strömmen eftersom det är en ersättningsresistans? Dessutom är alla fyra motstånden kopplade till varandra på ett eller annat sätt, varför tar man inte med att tex 25 motståndet egentligen inte bara är parallellkopplat till 40 motståndet utan även 8 motsåndet. Förlåt för att det är så många frågor.
Efter att man kopplat ihop punkterna P och Q så är resistorerna 25 och 15 inte längre seriekopplade. Seriekopplade resistorer kan man räkna på som man gör eftersom samma ström passerar bägge resistorerna. Det gör också att man kan lägga ihop, addera, summera, spänningen över de seriekopplade resistorerna. Parallellkopplade resistorer har samma spänning över sig, och man kan då lägga ihop, addera, summera strömmen som går igenom dessa. När P och Q har kopplats ihop så är spänningen samma över 25 och 40 ohms resistorerna, så de är parallellkopplade, och spänningen över 15 och 8 ohms resistorerna är också samma med varandra (inte med 25/40), så du kan lägga ihop strömmarna genom dessa när du räknar det som en parallellkoppling. Du har alltså en effektiv resistans över 25/40 där summan av strömmarna genom 25 och 40 ger samma spänning som finns över dessa motstånd. Samma argument gäller för 8/15.
Jag tror du letar lite efter en förklaring till varför det är en seriekoppling av parallellkopplingar och inte en parallellkoppling av seriekopplingarna. Det du har från början är en parallellkoppling av seriekopplingarna, och då måste samma ström gå genom 25 och 15 ohms motstånden, och den strömmen gånger summan av 25 och 15 ohm måste ge spänningen 24V. Någon annan ström måste gå genom både 40 och 8 ohms motstånden, och den strömmen måste ge spänningen 24V. Så fort du kopplar ihop P och Q så ändras reglerna -- du vet inte omedelbart vilken väg strömmen som går genom 25 ohms motståndet tar, men du vet att summan av stömmarna genom 25 och 40 måste gå vara samma som summan av strömmarna som går genom 15 och 8. Samma spänning och summan av strömmarna är parallellkoppling, samma ström och summan av spänningarna är seriekoppling. När du vet strömmen men inte vet vilken väg den tar genom - som du säger, summaströmmen är känd, men eftersom du känner motstånden så vet du relationen mellan strömmarna och kan plocka isär summaströmmen i respektive resistor.
