Bestämma tangentplan

Min tanke var att hitta de partiella derivatorna, för att sen kryssa dem för att få normalen till planet. Men jag trasslar ihop det tror jag.
Ungefär så här långt kommer jag:
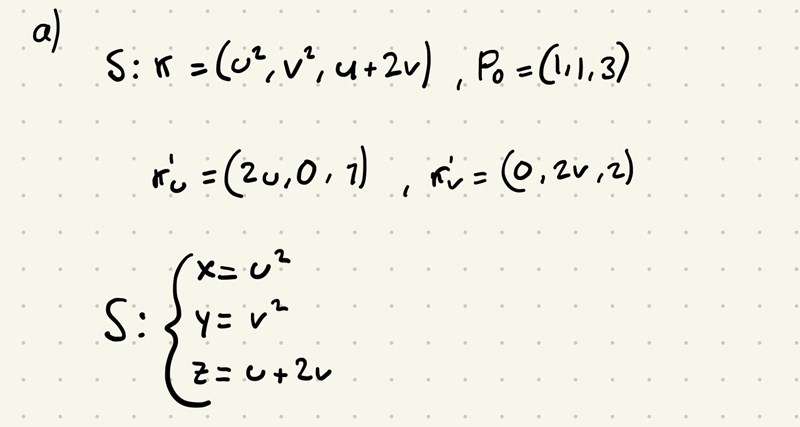
Ser bra ut så långt, kryssa vektorerna, räkna ut vilka värden och som ger
Vad blir alltså en normal till ytan där?
D4NIEL skrev:Ser bra ut så långt, kryssa vektorerna, räkna ut vilka värden och som ger
Vad blir alltså en normal till ytan där?
När jag kryssar vektorerna får jag en vektor . Vad betyder den här vektorn? Är detta normalen? Och hur får jag normalen i punkten P0?
Ja, det är normalen.
Sätt in de värden på och som ger
T.ex. ska tydligen osv.
D4NIEL skrev:Ja, det är normalen.
Sätt in de värden på och som ger
T.ex. ska tydligen osv.
Okej, alltså u = 1 och v = 1. Är normalen i punkten P0 lika med (-2,-4,4) då?
Japp. Andra parallella normaler är (-1,-2,2) och (1,2,-2).
D4NIEL skrev:Japp. Andra parallella normaler är (-1,-2,2) och (1,2,-2).
Tack!

