Bestämma tangentplan till en yta genom två punkter
Hej, Jag har sätt massa uppgifter här då man ska bestämma tangetplanets ekvation genom en punkt men inte genom två eller tre. Jag har följande uppgift; (2.51 primärt men även 2.52
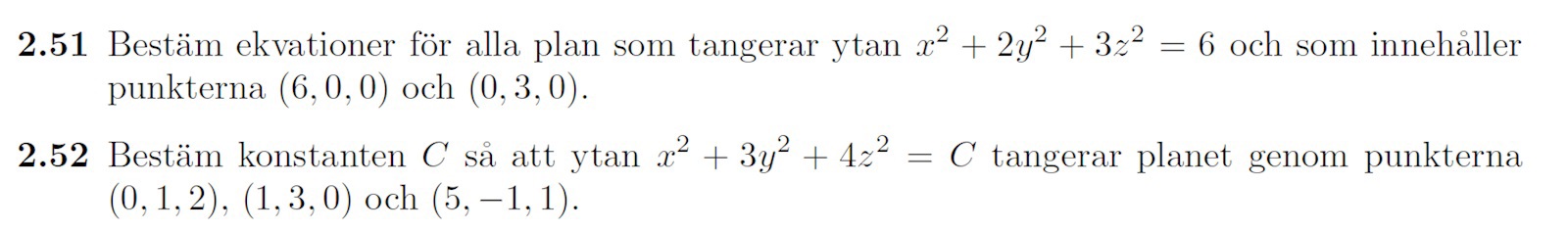
Jag har kommit fram till en gradient (2x,4y,6z) men har försökt olika metoder för att försöka få fram tangentplanets ekvation utan framgång. Mina tankegångar började med att försöka först skapa en vektor v som utgörs av de två punkterna, t.ex v = (6,-3,0) och sedan resonerat mig fram genom att säga, om vektorn v ligger i planet som tangerar ytan så måste v * n (v skalärt normalen) = 0. Kom inte långt med den metoden. Det jag försökte sedan (som visas nedan) var att lösa tangentplanekvationen två gånger för de två punkter som då ger ett ekvationsystem. Men avsaknaden av en z koordinat är det svårt att dra slutsatsen om vad den skulle vara. 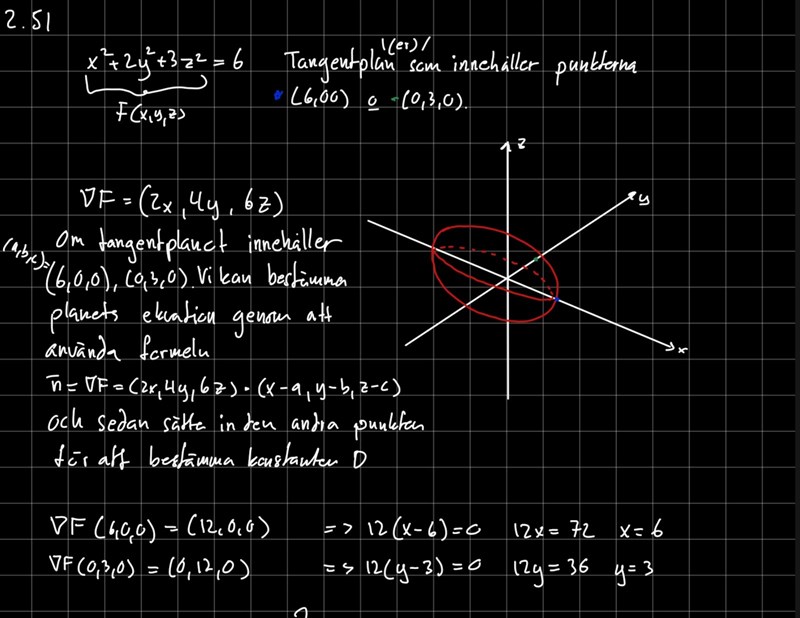
Har jag ens tänk rätt från början eller är jag helt ute och cyklar? Tacksam för hjälp.
Det blir lite överanvändning av x, y och z, vilket leder till lite förvirring.
Välj en punkt (a, b, c) på ellipsoiden.
En normalvektor till ellipsoiden i (a, b, c) ges av (2a, 4b, 6c) (mha gradienten). Ett tangentplan till ellipsoiden i (a, b, c) ges därför av
(2a, 4b, 6c)(x-a, y-b, z-c) = 0 (1).
Vi har kravet att punkterna (x, y, z) = (6, 0, 0) och (x, y, z) = (0, 3, 0) skall uppfylla planets ekvation (1), dvs ligga i planet. Detta ger två ekvationer för a, b och c som tillsammans med ekvationen för ellipsoiden (a2+2b2+3c2=6) gör att du kan hitta möjliga värden på a, b och c.
Säg till om du kör fast.
PATENTERAMERA skrev:Det blir lite överanvändning av x, y och z, vilket leder till lite förvirring.
Välj en punkt (a, b, c) på ellipsoiden.
En normalvektor till ellipsoiden i (a, b, c) ges av (2a, 4b, 6c) (mha gradienten). Ett tangentplan till ellipsoiden i (a, b, c) ges därför av
(2a, 4b, 6c)(x-a, y-b, z-c) = 0 (1).
Vi har kravet att punkterna (x, y, z) = (6, 0, 0) och (x, y, z) = (0, 3, 0) skall uppfylla planets ekvation (1), dvs ligga i planet. Detta ger två ekvationer för a, b och c som tillsammans med ekvationen för ellipsoiden (a2+2b2+3c2=6) gör att du kan hitta möjliga värden på a, b och c.
Säg till om du kör fast.
Tack! Jag tror jag gör uppgifter svårare för mig själv, med med det enkla ekvationssystem så löste det sig. Tog bara 2 dagar att inse :D.
Skönt att höra.


