Bestämma täthetsfunktion m.h.a. faltningsformeln: Varför är 1 en "magisk" gräns?

Du har inte fått något svar så jag skriver fastän mitt minne av faltningar är blekt. Läs på egen risk, jag kanske bara rör till det.

Vi lägger ihop två tal. X kan vara vilket positivt tal som helst, Y är mellan noll och ett. Hur ser fördelningen för summan ut? 

Min tanke är att man startar med Y. Låt Y gå från 0 till 1. För varje Y på vägen ser man hur fördelningen av X-värdena påverkar summan.

(Man kan förstås börja med X också, men det blir inte lika intuitivt.)

När Y har landat på 1 så är vi klara. Det verkar ganska naturligt att 1 är en viktig gräns. 

Nu betraktar jag raden i lösningen ”Om z > 1 så är…”:

Säg att Z = 3.

Om Y är noll så ska X vara 3, hur troligt är det?

Om Y = 0,4 så ska X vara 2,6, hur troligt är det?

Om Y = 1 så ska X vara 2, hur troligt är det?

Detta är slappt språkbruk, jag vet. Sannolikheten att Y = 0,4 och X = 2,6 är såklart noll, men vi jämför tätheter. Bortser vi från det omatematiska språket så tycker jag att min tankegång avspeglas i integralen;

Y (dvs u) glider från 0 till 1 och X tar värdet 3–Y i faktorn e^–(3–Y).

På nästa rad, ”för 0 ≤ z ≤ 1…” så har vi samma procedur, men nu får Y vara högst Z.

Jag tycker resonemanget går att förstå även för den som inte sett faltningar sedan Hedenhös. Men jag skriver som sagt omatematiskt, blandar säkert stora och små x, y, z, och talar om ”sannolikheter” där jag skulle varit tydligare. 

Jag förstår att bilden är relevant, men jag kan inte riktigt se hur den hjälper mig att skriva upp faltningsuttrycken.

Givet  $f_X(x)=e^{-x}$ för $x \ge 0$  och  $f_Y(y) = 1$ för $0 \le y \le 1$, så får man

$\displaystyle f_{X+Y}\left(z\right) = \int_{-\infty}^\infty f_X\left(z-u\right) f_Y\left(u\right)\,du$.

Nu är frågan vad $u$ ska vara så att båda faktorerna $f_X(z-u)$ och $f_Y(u)$ blir nollskilda:

• $f_Y(u) \neq 0$ kräver att $0 \le u \le 1$ (härifrån kommer det magiska värdet 1)
• $f_X(z-u) \neq 0$ kräver att $z-u \ge 0$, d.v.s.  $u \le z$.

Härmed har integrationsgränserna hittats:

• $u=0$ är undre integrationsgränsen
• Eftersom $u\le 1$ och samtidigt $u\le z$ krävs, så är det det minsta av $1$ och $z$ som är övre integrationsgränsen.

(Om $z \le 0$, så finns det inget utrymme för $u$ som ska ligga ovanför $0$ dock under $z$, så $f_{X+Y}(z) = 0$ då $z \le 0$)

Det kan bli lite besvärligt att beräkna integralen där övre integrationsgränsen är antingen 1 eller z beroende på vad som är minst, så man gör en falluppdelning. Antingen är 1:an minst (d.v.s. $1 \le z$), eller så är $z$:t minst (d.v.s. $z < 1$)

Även om det är sant per definition så borde nedre gränsen i

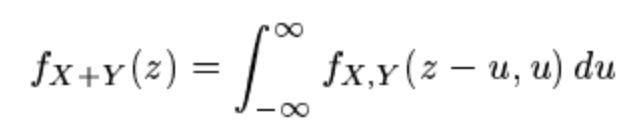
vara 0 då det på raden ovan konstateras att X+Y ligger i [0,oo).

Coffeeshot, har du fått svar på frågan vad det är som gör talet 1 så speciellt?

Vi söker fördelningen för summan Z. Om Z är mindre än 1 så kan både X och Y variera från 0 till Z. Om X är större än 1 så kan X bara variera mellan Z–1 och Z, samt Y bara mellan 0 och 1. 

Jag har fått svar! Ni hjälpte mig dessutom att inse hur jag ska tänka när man använder faltningsformeln. Enormt hjälpsamt. Tack så jättemycket!