Bestämma vinkel v (bisektriser)
I en triangel är två bisektriser inritade som figuren visar. Bestäm vinkeln v.
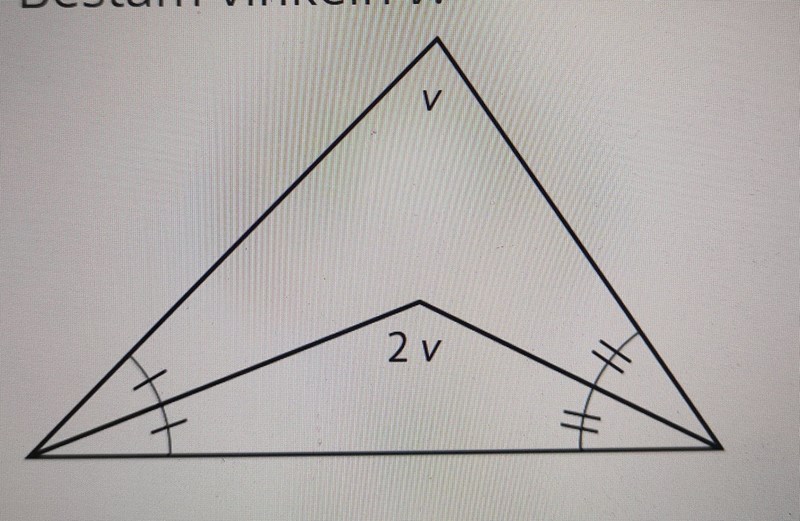
Följande tips ges i samband med uppgiften; "Ställ upp en ekvation för vinkelsumman i den stora triangeln respektive i den lilla triangeln."
Typ såhär?
Triangel A: 180= v + 2x + 2y
Triangel B: 180°= 2v + x + y
Nja, det känns inte korrekt och jag kommer inte vidare med den ekvationen...
Någon som vet vad det är jag saknar? Tack på förhand
Ekvationerna är korrekta. Men rita gärna en figur där det framgår vilken vinkel som är x respektive y.
Finns det mer information i uppgiften som du har glömt att skriva eller är det allt?
Då du införde den mindre triangeln i den stora triangeln så skapade du även en fyrhörning, vars vinkelsumma blir 360 grader. Kan du sätta upp ett uttryck som säger detta?
Alternativ lösning:
Låt u=x+y. Dina ekvationer blir då
Du har gjort helt rätt. Lös ut v ur den ena och sätt in i den andra. Då kan du ta reda på hur mycket t.ex x+y är. Vad säger det om 2v?
Bo-Erik skrev:Ekvationerna är korrekta. Men rita gärna en figur där det framgår vilken vinkel som är x respektive y.
Finns det mer information i uppgiften som du har glömt att skriva eller är det allt?
Här är en förtydling. Jag har godtyckligt benämnt vinkel x samt y, samt döpt de båda trianglarna till A resp B.
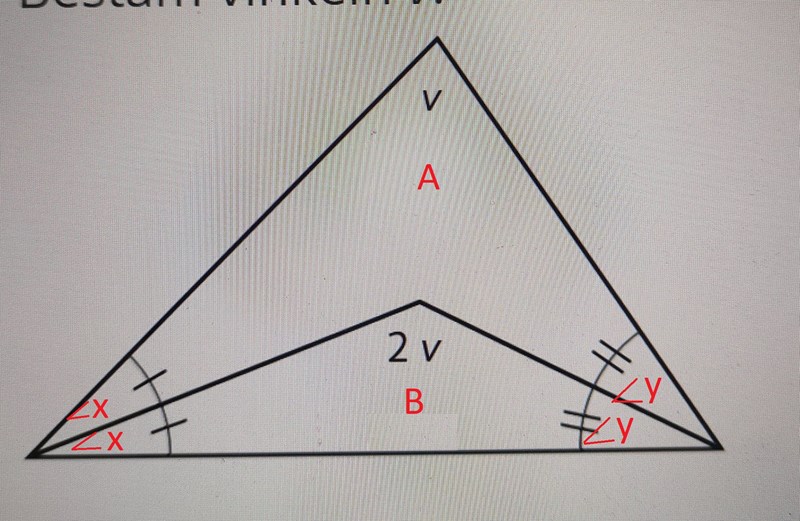
Bedinsis skrev:Då du införde den mindre triangeln i den stora triangeln så skapade du även en fyrhörning, vars vinkelsumma blir 360 grader. Kan du sätta upp ett uttryck som säger detta?
Menar du BC/CD = AB/AC?
Jag är inte helt säker på hur man tillämpar den regeln...
Jag menar nedanstående fyrhörning. Eftersom en fyrhörning av nödvändighet består av två trianglar är dess vinkelsumma 2*180= 360. Och du har redan en beteckning på de flesta av dess vinklar.
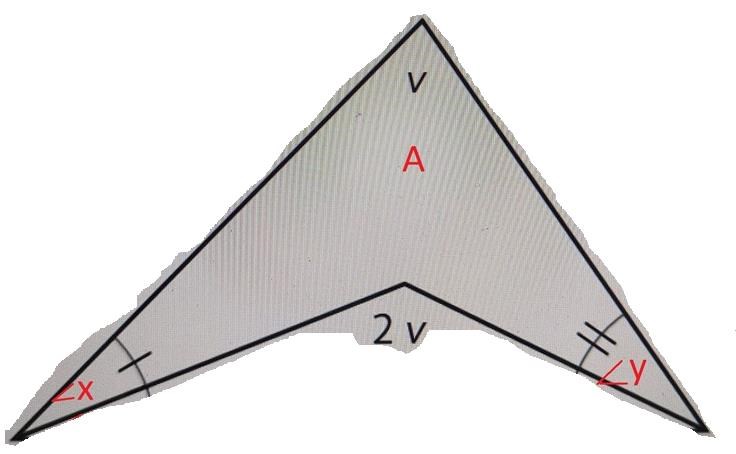
Jroth skrev:Alternativ lösning:
Låt u=x+y. Dina ekvationer blir då
Tack, detta fick poletten att trilla ned!
180=2v+u <-> u=180-2v
180=v+2u <-> 180=v+360-4v <-> 3v=180 <-> v=60
Bedinsis skrev:Jag menar nedanstående fyrhörning. Eftersom en fyrhörning av nödvändighet består av två trianglar är dess vinkelsumma 2*180= 360. Och du har redan en beteckning på de flesta av dess vinklar.
Jag är intresserad utav lösningen men jag vet inte hur jag ska applicera ekvationen jag får.
360=3v+x+y
Vad ställer jag upp ekvationen mot för att lösa den?
Mvh
2v är inte vinkeln på insidan av fyrhörningen, det är vinkeln på utsidan.
Såg precis att du egentligen redan hittat lösningen. Jag tänkte därför skriva ner vad jag tänkte:
Eftersom vinkeln på utsidan är 2v måste vinkeln på insidan vara 360-2v. Detta ger:
360= v+x+y+(360-2v)
360-360=x+y+v-2v
0=x+y-v
v=x+y
Den mindre triangeln ger
180=2v+x+y
180=2v+v=3v
v=60
vilket du redan kommit fram till.


