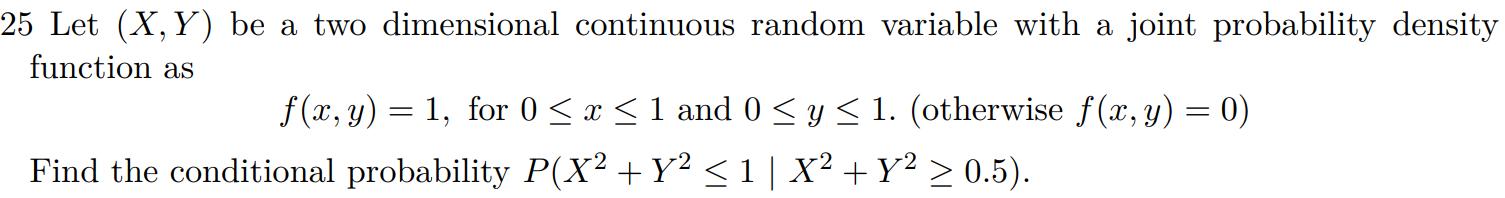Betingad sannolikhet med stokastiska variabler

jonte12 skrev:

Jag tänker såhär:

Svaret ska bli 0,647. Hur kommer det sig?

Vad är det du har i nämnaren? Skall inte den vara 1?

Smaragdalena skrev:

jonte12 skrev:

Jag tänker såhär:

Svaret ska bli 0,647. Hur kommer det sig?

Vad är det du har i nämnaren? Skall inte den vara 1?

Jag tänker att jag använder den här formeln

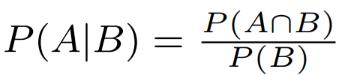
Jag är lite osäker på din skiss. Den gröna termen är sannolikheten att x^2+y^2 är STÖRRE än 0.5, så för mig borde det vara inom kvadraten men utanför det som du nu ritat som grönt (dvs komplementet till det du ritat/skrivit nu).

Vid närmare eftertanka skall nämnaren inte vara 1.

Och en ytterligare kommentar: kom ihåg att x^2+y^2=r^2. Så om x^2+y^2=0.5 betyder det att det är en cirkel med radie $\sqrt{0.5}$. Det var en detalj jag glömde

Nej, här är det lätt att gå vilse i beteckningarna. Det är inte x² + y² som ska vara mer än 0.5, det är X² + Y².

Om vi vet att X² + Y² är minst 0.5, vad är det egentligen vi vet då?

Bubo skrev:

Nej, här är det lätt att gå vilse i beteckningarna. Det är inte x² + y² som ska vara mer än 0.5, det är X² + Y².

Om vi vet att X² + Y² är minst 0.5, vad är det egentligen vi vet då?

Ok visst jag borde använt stora bokstäver ibland, men jag är det något fel på mitt resonemang? f(x,y)=1 så i princip behöver vi bara hitta arean på två områden (integrera funktionen 1 över två områden), dividera dem och så har vi svaret? 

Visst, jag tror att du har alldeles rätt. Just nu försöker jag räkna fram 0.647 men misslyckas.

Bubo skrev:

Visst, jag tror att du har alldeles rätt. Just nu försöker jag räkna fram 0.647 men misslyckas.

Ok, jag fick 0.64663014638 (vilket jag avrundar till 0.647) när jag tillslut satte in att radien på cirklarna var 1 respektive $\sqrt{0.5}$....

Just det - radien är roten ur 0.5. Tack.