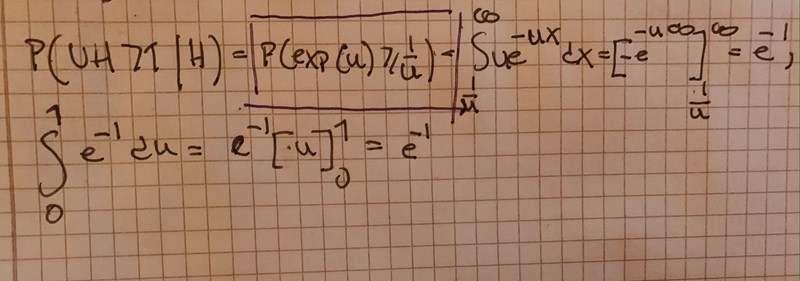betingat väntevärdet och varians

Jag vet exakt hur man ska göra.

Men det blir mer lärorikt tror jag om du visar lite vad du gjort.

jag löste det !! :D

däremot undrar jag om denna fråga som tillhör ovanstående:

b) Beräkna sannolikheten att en sida av tornet har yta större än 1 areaenhet, alltså P(UH ≥ 1).

Hur jag gör jag för att hitta gränsen för första integralen? j

Det är svårt att hjälpa när du ger mig så lite info om vad du gjort.

När jag löser den uppgiften så är det bara en integral, och den går från 0 till 1 men vad du menar med den "första integralen" är helt omöjligt för mig att veta.

jag förstår inte hur man kom fram till gränsen som jag gjort en ruta kring. Efter jag kollade i facit och såg facit förstod jag helt hur jag skulle göra, mest med gränserna som gjorde det krånligt

Du har ju rent generellt:

Om den kontinuerliga slumpvariabeln  X är definierad på (a,b) och har täthetsfunktion f(x) så är sannolikheten 

$P(X\ge t)={\int }_t^{b}f\left(x\right)dx.$

I det här fallet är X (den exponentialfördelade variabeln) definierad på $(0,\infty )$så vi får:

$P(X\ge \frac{1}{u})={\int }_{1/u}^{\infty }f\left(x\right)dx$

är fof inte med på hur den undre gränsen blir 1/u?

Vi vill veta

$P(UH>1|U)=P(H>1/U\left|U\right)$

Givet U är H~ exp(U). Med andra ord söker vi sannolikheten att en exp(U) är större än 1/U.

Att detta blir en integral som börjar i 1/U är liksom själva kärnegenskapen för vad en täthetsfunktion är. Alltså om variabeln X har fördelningen f(x) så är 

$P(a\le X\le b)={\int }_a^{b}f\left(x\right)dx.$