Bevis

Då får du väl pröva att gå från andra hållet.
Utveckla de båda termerna i HL och förenkla dem så långt det går.
Försök sedan faktorisera summan och se om du kan få ihop produkten till ett uttryck = (n över 4).

Att påståendet är sant vet vi ju från Pascals triangel.

jag gjorde det och förlängde båda till gemensam nämnare 12, men fick något konstigt svar sedan och visste inte hur jag skulle fortsätta/vart jag gjort fel?

melinasde skrev:

jag gjorde det och förlängde båda till gemensam nämnare 12, men fick något konstigt svar sedan och visste inte hur jag skulle fortsätta/vart jag gjort fel?

Visa ditt försök så kan vi hjälpa dig att hitta felet.

Du kan skriva för hand och ladda upp en bild om du vill.

Menar du att uppgiften är

Visa att $\left(\begin{array}{c}n\\ 4\end{array}\right)=\left(\begin{array}{c}n-1\\ 4\end{array}\right)+\left(\begin{array}{c}n-1\\ 3\end{array}\right)$?

I så fall skulle jag börja med att utveckla HL och se om jag kan få det att bli till VL. Det är ofta (men inte alltid...) en bra idé att börja på den sidan som ser krångligast ut, och det tycker jag är HL.

Det här är min påbörjade lösning, blir ju dock ej som HL? Kan du hjälpa mig?

Du gör fel när du bryter ut! Du kan inte bryta ut (n-3)! som du skriver att du gör. Det du kan bryta ut är (n-1)(n-2)(n-3), men det är inte samma sak som (n-3)!

(Om du undrar varför, sätt n=6 och jämför (n-3)! med (n-1)(n-2)(n-3))

Gjorde såhär nu men kommer inte längre?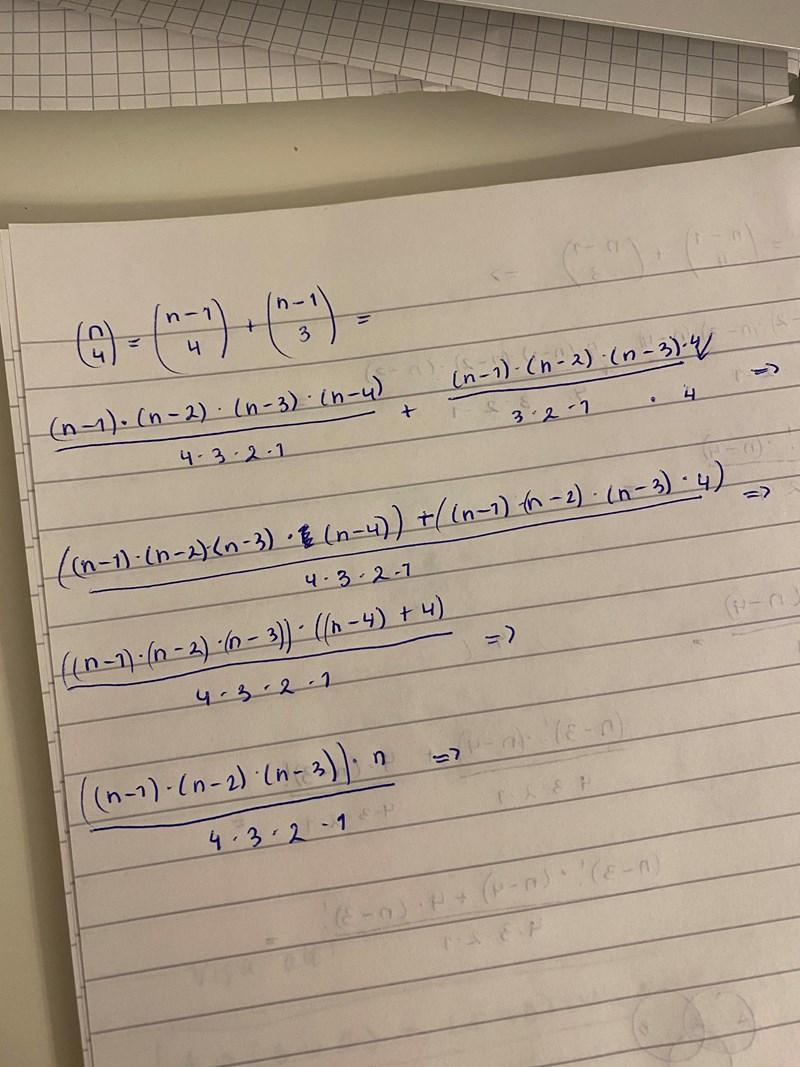

Du behöver inte komma längre, du är ju framme nu ;)

Jämför det du har skrivit med $\left(\begin{array}{c}n\\ 4\end{array}\right)$

men va det är väl inte samma eller? (n över 4) är ju ( n-1 x n-2 x n-3 x n-4 / 4x3x2x1) och jag har inget n-4 i täljaren i mitt svar?

SvanteR skrev:

Du behöver inte komma längre, du är ju framme nu ;)

Jämför det du har skrivit med $\left(\begin{array}{c}n\\ 4\end{array}\right)$

jag skojade bara, trodde det stod n-1 i täljaren! Tack så mycket för hjälpen :)