Bevis att högerledet är lika med vänsterledet i det givna uttrycket

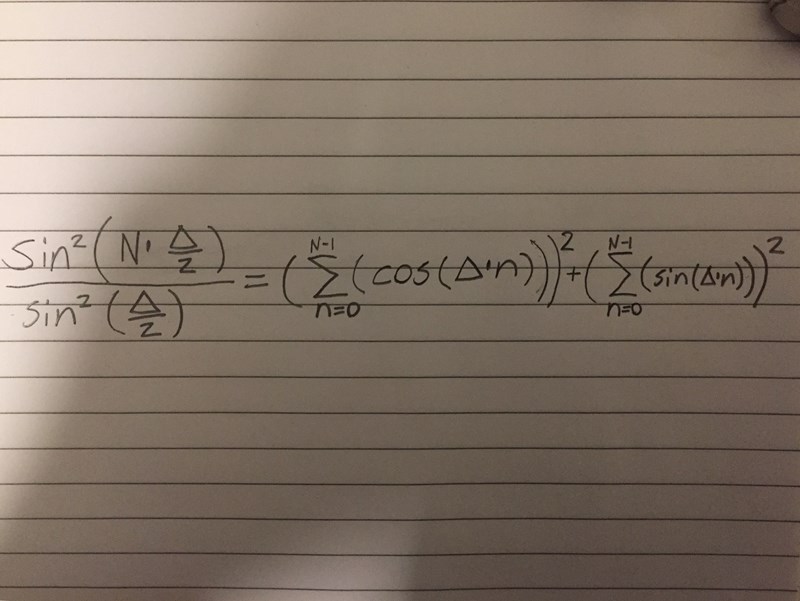
Jag tycker att induktion är rimligt...

Är det någon speciell anledning att du använder stora delta?

Qetsiyah skrev:

Jag tycker att induktion är rimligt...

Är det någon speciell anledning att du använder stora delta?

Ja, jag håller med men har aldrig bevisat en så här svår induktion tror jag.

Nej, jag använde det bara som beteckning på variabeln.

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Åh... genialt!

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Geometrisk summa

$\sum _{n=0}^{N-1}{q}^n=\frac{q^N-1}{q-1}$, och således

$z=\frac{e^{iN\Delta }-1}{e^{i\Delta }-1}$.

Följande formel blir sedan användbar

$$\begin{gathered} \left(e^{ix}-1\right)\left(e^{-ix}-1\right)=\left(\cos \right(x)+i\sin (x)-1)\left(\cos \right(x)-i\sin (x)-1)= \\ 2(1-\cos (x\left)\right)=4{\sin }^2(x/2) \end{gathered}$$

PATENTERAMERA skrev:

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Geometrisk summa

$\sum _{n=0}^{N-1}{q}^n=\frac{q^N-1}{q-1}$, och således

$z=\frac{e^{iN\Delta }-1}{e^{i\Delta }-1}$.

Följande formel blir sedan användbar

$$\begin{gathered} \left(e^{ix}-1\right)\left(e^{-ix}-1\right)=\left(\cos \right(x)+i\sin (x)-1)\left(\cos \right(x)-i\sin (x)-1)= \\ 2(1-\cos (x\left)\right)=4{\sin }^2(x/2) \end{gathered}$$

Smart, tack!

Einstein Euler skrev:

PATENTERAMERA skrev:

Visa föregående citat

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Geometrisk summa

$\sum _{n=0}^{N-1}{q}^n=\frac{q^N-1}{q-1}$, och således

$z=\frac{e^{iN\Delta }-1}{e^{i\Delta }-1}$.

Följande formel blir sedan användbar

$$\begin{gathered} \left(e^{ix}-1\right)\left(e^{-ix}-1\right)=\left(\cos \right(x)+i\sin (x)-1)\left(\cos \right(x)-i\sin (x)-1)= \\ 2(1-\cos (x\left)\right)=4{\sin }^2(x/2) \end{gathered}$$

Smart, tack!

Är dock ändå intresserad om någon kan lösa denna med hjälp av induktion eller liknande då jag tycker det rent intuitivt är lättare att första när man endast använder reella tal i beräkningar

Einstein Euler skrev:

Einstein Euler skrev:

Visa föregående citat

PATENTERAMERA skrev:

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Geometrisk summa

$\sum _{n=0}^{N-1}{q}^n=\frac{q^N-1}{q-1}$, och således

$z=\frac{e^{iN\Delta }-1}{e^{i\Delta }-1}$.

Följande formel blir sedan användbar

$$\begin{gathered} \left(e^{ix}-1\right)\left(e^{-ix}-1\right)=\left(\cos \right(x)+i\sin (x)-1)\left(\cos \right(x)-i\sin (x)-1)= \\ 2(1-\cos (x\left)\right)=4{\sin }^2(x/2) \end{gathered}$$

Smart, tack!

Är dock ändå intresserad om någon kan lösa denna med hjälp av induktion eller liknande då jag tycker det rent intuitivt är lättare att första när man endast använder reella tal i beräkningar

Ett geometriskt bevis finns här:

http://www.feynmanlectures.caltech.edu/I_30.html

Vet inte om det kan bli mer intuitivt.

PATENTERAMERA skrev:

Einstein Euler skrev:

Visa föregående citat

Einstein Euler skrev:

PATENTERAMERA skrev:

Visa föregående citat

PATENTERAMERA skrev:

Använd komplexa tal plus formeln för geometrisk summa.

$$\begin{gathered} z=\sum _{n=0}^{N-1}{e}^{in\Delta } \\ HL = zz* \end{gathered}$$

Geometrisk summa

$\sum _{n=0}^{N-1}{q}^n=\frac{q^N-1}{q-1}$, och således

$z=\frac{e^{iN\Delta }-1}{e^{i\Delta }-1}$.

Följande formel blir sedan användbar

$$\begin{gathered} \left(e^{ix}-1\right)\left(e^{-ix}-1\right)=\left(\cos \right(x)+i\sin (x)-1)\left(\cos \right(x)-i\sin (x)-1)= \\ 2(1-\cos (x\left)\right)=4{\sin }^2(x/2) \end{gathered}$$

Smart, tack!

Är dock ändå intresserad om någon kan lösa denna med hjälp av induktion eller liknande då jag tycker det rent intuitivt är lättare att första när man endast använder reella tal i beräkningar

Ett geometriskt bevis finns här:

http://www.feynmanlectures.caltech.edu/I_30.html

Vet inte om det kan bli mer intuitivt.

Är detta ett bevis med Feyman som upphovsman?

PATENTERAMERA skrev:

Ett geometriskt bevis finns här:

http://www.feynmanlectures.caltech.edu/I_30.html

Vet inte om det kan bli mer intuitivt.

Tack! Tycker det är mycket lättare att förstå nu