Bevis: Formulera och bevisa Cauchys integralformel.
Vill som sagt bara kolla så att jag får allting med, och att allt står rätt till. Detta är en tentafråga, så var kritiska ^^
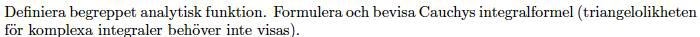
Sats: Låt vara en sluten kurva i positiv riktning som begränsar ett sammanhängande mängd,D. Som är analytisk till då gäller:
Bevis: Om vi byter ut mot cirkeln som ges av , så att blir innesluten i D. så får vi
$$\int_{\Gamma} \frac{f(z) dz}{z-z_0} = \int_{\gamma_{\epsilon}} \frac{f(z) dz}{z-z_0}$$ så:
Och vi vet att
Maclaurin uppskattningen ger
då
Där $$M_{\epsilon} är maximum på $$\gamma_{\epsilon}$$
Jag tycker du missar en viktig del i formuleringen, nämligen att funktionen skall vara analytisk på området samt att måste ligga inuti .
Sen vet jag inte om det krävs av uppgiften att du skall bevisa att det är giltigt att byta ut mot , men jag skulle göra det för att vara på säkra sidan.
Du borde även visa hur du får att:
Det sista du skriver begriper jag inte. Maclaurinuppskattning av vadå? Hur ger det att det är större än maxvärdet på kurvan? Varför går maxvärdet mot noll när går mot noll?
Slutligen behöver du också tydliggöra att du faktiskt bevisat formeln.
AlvinB skrev:Jag tycker du missar en viktig del i formuleringen, nämligen att funktionen skall vara analytisk på området samt att måste ligga inuti .
Sen vet jag inte om det krävs av uppgiften att du skall bevisa att det är giltigt att byta ut mot , men jag skulle göra det för att vara på säkra sidan.
Du borde även visa hur du får att:
Det sista du skriver begriper jag inte. Maclaurinuppskattning av vadå? Hur ger det att det är större än maxvärdet på kurvan? Varför går maxvärdet mot noll när går mot noll?
Slutligen behöver du också tydliggöra att du faktiskt bevisat formeln.
ML-uppskattnig menar jag ** (maxililkihood)
Hur skulle man bevisa att man får byta ut mot ?
Meeen gjorde jag inte så att jag visade = 2\pi i $$ väl? =/
Kommer inte riktigt ihåg vilket universtitet jag fann den här på,
Det är viktigt att du inte bara kopierar saker till höger och vänster när du skriver bevis. Är det något du inte skriver på pappret ska det vara självklart för dig varför det är så. Annars bör det definitivt förklaras i beviset.
1. Jag tror inte du menar Maximum likelihood-uppskattning (det är nåt inom statistik). Jag tror du pratar om följande uppskattning för en kurvintegral:
där är det största funktionsvärdet på kurvan och är kurvans längd. I ditt fall är (cirkel med radie ) vilket ger:
där betecknar det största värdet antar på kurvan .
Sedan kan du använda relationen
och låta vilket ger Cauchys integralformel.
2. är en sluten kurva som innesluter . Det kan se ut ungefär så här:

Säg då att vi drar en cirkel kring och lägger till två vertikala linjestycken. Då får vi:

De vertikala linjestyckena kommer ta ut varandra (i och med att de genomlöps två gånger åt motsatta håll) och vi blir kvar med (minustecknet kommer eftersom genomlöps åt fel håll). Eftersom diskontinuiteten hos integranden inte innesluts av dessa kurvor ger Cauchys integralsats:
Således har kurvintegralerna för de båda kurvorna samma värde. Samma resonemang fungerar för i stort sett alla slutna kurvor och integrander så länge kurvan innesluter diskontinuiteten.
3. Det är ganska enkelt att visa genom att parametrisera kurvan. En cirkel med radie centrerad i parametriseras av:
Då blir integralen:
Cauchys integralformel.
- Låt vara en funktion som är analytisk på en öppen delmängd () till det komplexa talplanet .
- Låt vara en cirkelskiva som ligger helt inuti mängden .
Funktionens värden inuti cirkelskivan bestäms helt och hållet av funktionens värden på cirkelskivans positivt orienterade rand ().
Beviset av Cauchys integralformel bygger på Cauchys integralsats (som är den viktigaste satsen inom komplex analys).
Cauchys integralsats.
- Låt vara en funktion som är analytisk på en öppen delmängd () till det komplexa talplanet
- Låt definitionsmängden vara en enkelt sammanhängande mängd.
- Låt vara en enkel sluten kurva som ligger helt inuti mängden .
.
Notera att funktionen är inte analytisk på cirkelskivan , eftersom punkten ligger inuti cirkelskivan och nämnaren blir noll när ; därför kan man inte använda i Cauchys integralsats.
Däremot kan man använda Cauchys integralsats på funktionen om man utesluter den farliga punkten ; det gör man lämpligen genom att omringa punkten med en liten cirkelskiva med liten radie .
Den ihåliga cirkelskivan är en enkelt sammanhängande mängd och dess rand är en enkel sluten kurva som ligger helt inuti den öppna mängden . Då ger Cauchys integralsats
.
Det återstår att visa att oavsett hur liten radien än är så är linjeintegralen
.
AlvinB skrev:Det är viktigt att du inte bara kopierar saker till höger och vänster när du skriver bevis. Är det något du inte skriver på pappret ska det vara självklart för dig varför det är så. Annars bör det definitivt förklaras i beviset.
1. Jag tror inte du menar Maximum likelihood-uppskattning (det är nåt inom statistik). Jag tror du pratar om följande uppskattning för en kurvintegral:
där är det största funktionsvärdet på kurvan och är kurvans längd. I ditt fall är (cirkel med radie ) vilket ger:
där betecknar det största värdet antar på kurvan .
Sedan kan du använda relationen
och låta vilket ger Cauchys integralformel.
2. är en sluten kurva som innesluter . Det kan se ut ungefär så här:
Säg då att vi drar en cirkel kring och lägger till två vertikala linjestycken. Då får vi:
De vertikala linjestyckena kommer ta ut varandra (i och med att de genomlöps två gånger åt motsatta håll) och vi blir kvar med (minustecknet kommer eftersom genomlöps åt fel håll). Eftersom diskontinuiteten hos integranden inte innesluts av dessa kurvor ger Cauchys integralsats:
Således har kurvintegralerna för de båda kurvorna samma värde. Samma resonemang fungerar för i stort sett alla slutna kurvor och integrander så länge kurvan innesluter diskontinuiteten.
3. Det är ganska enkelt att visa genom att parametrisera kurvan. En cirkel med radie centrerad i parametriseras av:
Då blir integralen:

https://people.kth.se/~haakanh/courses/SF1628/SF1628-2017/Lectures/SF1628-F7.pdf
Hitta den! :D
Men så säger man då "ML uppskattning"?
Jo, ML-uppskattning, inte Maximum-likelihood.
Men det där beviset är inte fullständigt. Du måste ju även förklara varför
bevisar Cauchys integralformel.
Jag tycker även att du kan utveckla hur du får olikheten med . För att få fram det krävs nämligen mer än att bara göra en ML-uppskattning av integralen.
Albiki skrev:Den ihåliga cirkelskivan är en enkelt sammanhängande mängd och dess rand är en enkel sluten kurva som ligger helt inuti den öppna mängden . Då ger Cauchys integralsats
.
Det återstår att visa att oavsett hur liten radien än är så är linjeintegralen
.
Man kan skriva vilket visar att linjeintegralen kan skrivas som en summa av två linjeintegraler längs den lilla cirkeln .
Den första termen är lika med och den andra termen är lika med noll.
Det första termen beräknas genom att parametrisera den lilla cirkeln
Det betyder att när så är och differentialen
vilket ger linjeintegralen
För att visa att den andra termen är lika med noll visar man att
där är en viss konstant.
Man noterar att denna olikhet ska gälla oavsett hur liten cirkelns radie än är; den enda möjligheten för olikheten att gälla under sådana omständigheter är om linjeintegralen hela tiden är lika med noll.
För att få en övre begränsning till linjeintegralens modul kan man göra följande uppskattning
.
Notera att när så ligger på enhetscirkeln så att dess modul är , vilket ger linjeintegralen
och den övre begränsningen
Om man kan visa att
där konstanten inte beror på cirkeln så är beviset av Cauchys integralformel klart.
Albiki skrev:För att få en övre begränsning till linjeintegralens modul kan man göra följande uppskattning
.
Notera att när så ligger på enhetscirkeln så att dess modul är , vilket ger linjeintegralen
och den övre begränsningen
Det här låter konstigt. Varför ligger på enhetscirkeln? Det borde väl snarare vara så att ligger på en cirkel med radie centrerad i origo. Då blir och
AlvinB skrev:Albiki skrev:För att få en övre begränsning till linjeintegralens modul kan man göra följande uppskattning
.
Notera att när så ligger på enhetscirkeln så att dess modul är , vilket ger linjeintegralen
och den övre begränsningen
Det här låter konstigt. Varför ligger på enhetscirkeln? Det borde väl snarare vara så att ligger på en cirkel med radie centrerad i origo. Då blir och
Ja, det stämmer. Det var fel av mig. Då måste man korrigera mitt efterföljande inlägg också till att visa att
för någon konstant som inte beror på cirkeln .
Albiki skrev:Om man kan visa att
där konstanten inte beror på cirkeln så är beviset av Cauchys integralformel klart.
Så.. räcker det med att man bara säger det där, så är det bra? (Som komplement till det som jag postade fr KTH)
mrlill_ludde skrev:Albiki skrev:Om man kan visa att
där konstanten inte beror på cirkeln så är beviset av Cauchys integralformel klart.
Så.. räcker det med att man bara säger det där, så är det bra? (Som komplement till det som jag postade fr KTH)
Nej, det räcker inte att bara säga det; du ska även bevisa att så är fallet. Du har citerat fel inlägg. Det du ska visa är att
Fundera på vad du vet om funktionen och se hur denna kunskap kan hjälpa dig att visa olikheten.


