Bevis geometri
Hej,
jag har problem med denna uppgift:
"En linje genom en triangel delar två av triangelns sidor mitt itu. Visa att linjen är parallell men triangelns tredje sida."
Detta enda jag kan komma på är att visa att transversalsatsen gäller, därav så är den tredje sidan parallell. Men jag är osäker om det faktiskt bevisar någor.
Tack på förhand!
Habbe skrev:Hej,
jag har problem med denna uppgift:
"En linje genom en triangel delar två av triangelns sidor mitt itu. Visa att linjen är parallell men triangelns tredje sida."
Detta enda jag kan komma på är att visa att transversalsatsen gäller, därav så är den tredje sidan parallell. Men jag är osäker om det faktiskt bevisar någor.
Tack på förhand!
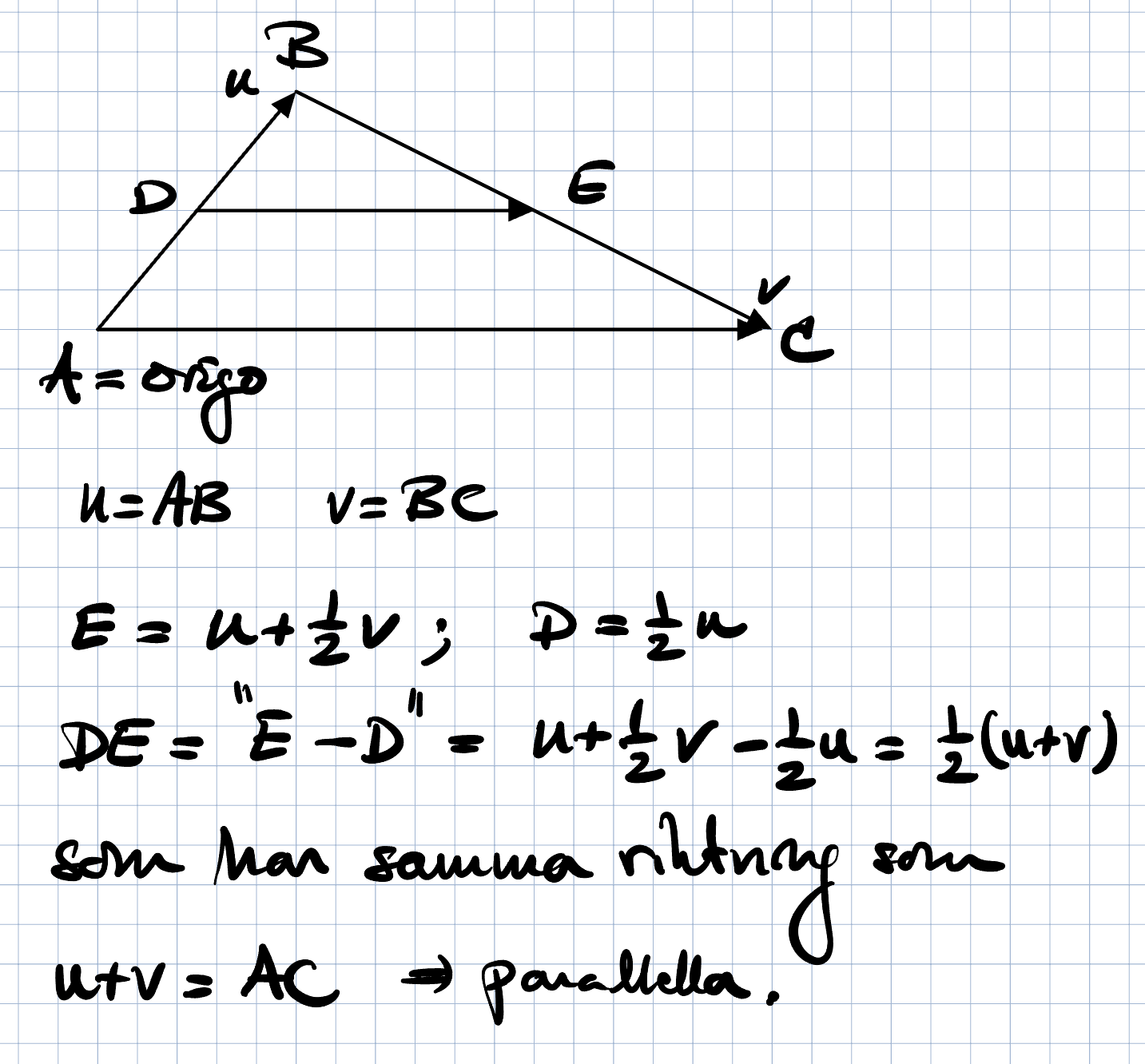
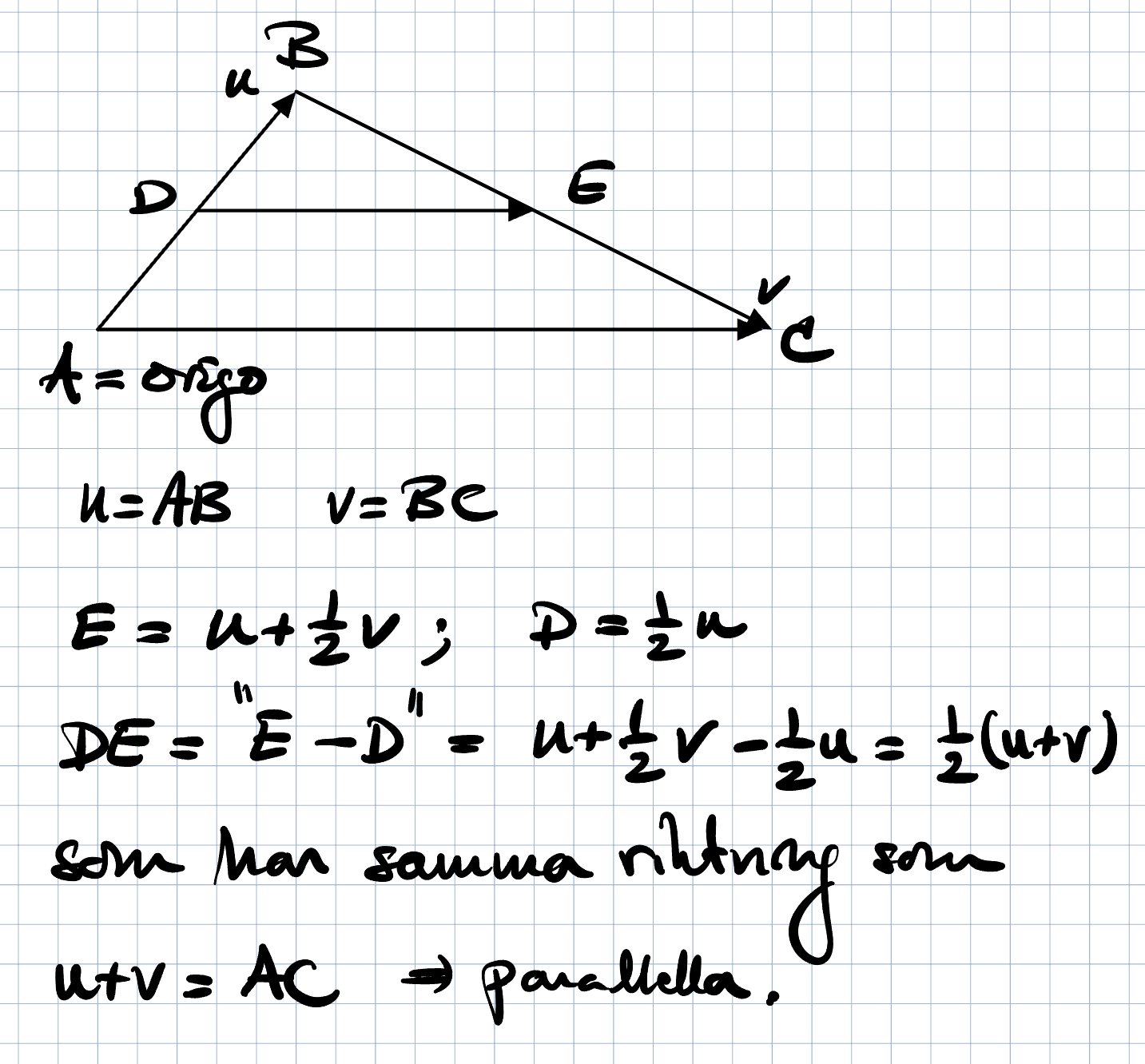
Du anger ”geometri” men kanske vektorer accepteras?
Trinity2 skrev:Habbe skrev:Hej,
jag har problem med denna uppgift:
"En linje genom en triangel delar två av triangelns sidor mitt itu. Visa att linjen är parallell men triangelns tredje sida."
Detta enda jag kan komma på är att visa att transversalsatsen gäller, därav så är den tredje sidan parallell. Men jag är osäker om det faktiskt bevisar någor.
Tack på förhand!
Du anger ”geometri” men kanske vektorer accepteras?
Tack för svaret!
Vi har inte riktigt kommit till vektorer ännu, kapitelet heter "Likformighetsfallen" kan jag tillägga. Det lär ju finnas ett sätt att bevisa det med geometri tänker jag.
Habbe skrev:Trinity2 skrev:Habbe skrev:Hej,
jag har problem med denna uppgift:
"En linje genom en triangel delar två av triangelns sidor mitt itu. Visa att linjen är parallell men triangelns tredje sida."
Detta enda jag kan komma på är att visa att transversalsatsen gäller, därav så är den tredje sidan parallell. Men jag är osäker om det faktiskt bevisar någor.
Tack på förhand!
Du anger ”geometri” men kanske vektorer accepteras?
Tack för svaret!
Vi har inte riktigt kommit till vektorer ännu, kapitelet heter "Likformighetsfallen" kan jag tillägga. Det lär ju finnas ett sätt att bevisa det med geometri tänker jag.
Så här kanske?