Bevis linjär algebra
Hej,
I min kursbok går de igenom nedanstående fråga:
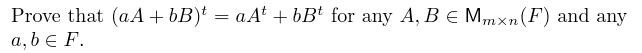
Och bevisar även denna, det jag inte förstår är vad i respektive j betyder i beviset - är de andra uttryck för m och n? Och är det i så fall dessa man bör använda när man gör ett bevis?
Och är aij x Aij kryssprodukten eller multiplikation?
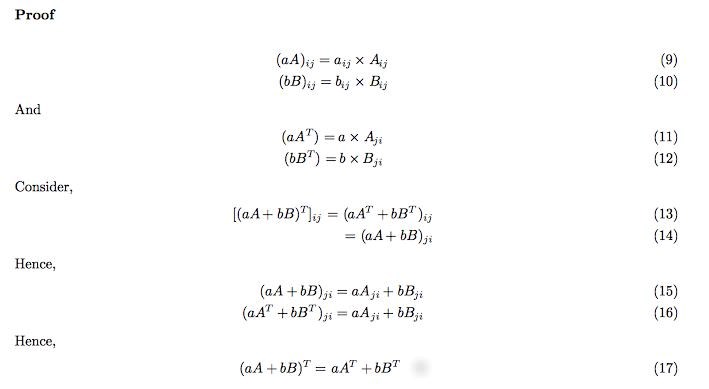
Hej!
och är index som visar på elementet på plats i matrisen. Alltså har vi att och . Vi kan hitta alla element i matrisen med hjälp av dessa index.
Ex:
Låt . Då gäller exempelvis att och .
Eftersom (där jag antar att är en kropp) så gäller att dom bara är skalärer, vanliga tal. Alltså kan inte vara en kryssprodukt eftersom är en skalär och är en matris (vi definierar bara kryssprodukt mellan två vektorer i .
Jag håller med att det är lite konstigt att skriva eftersom inte beror på några index, men men.
Moffen skrev:Hej!
och är index som visar på elementet på plats i matrisen. Alltså har vi att och . Vi kan hitta alla element i matrisen med hjälp av dessa index.
Ex:
Låt . Då gäller exempelvis att och .
Eftersom (där jag antar att är en kropp) så gäller att dom bara är skalärer, vanliga tal. Alltså kan inte vara en kryssprodukt eftersom är en skalär och är en matris (vi definierar bara kryssprodukt mellan två vektorer i .
Jag håller med att det är lite konstigt att skriva eftersom inte beror på några index, men men.
Hej Moffen,
Stort tack för att du tog dig tid att förklara detta! Nu förstår jag mycket tydligare och kan äntligen fortsätta att räkna vidare.
Ja lite konstigt är det, men bra iallafall att jag nu vet vad aij betyder.
Tack igen!
Hej Lund,
En matris av typ har stycken rader och stycken kolumner. Matriselementet (talet) som finns på rad nummer och kolumn nummer är och man länkar ihop matrisen med dess element via beteckningen
Transponatet är en matris av typ och matriselementet ges av
Detta medför att matrisen har matriselementen
vilket visar sambandet

