Bevisa att √2 är irrationellt

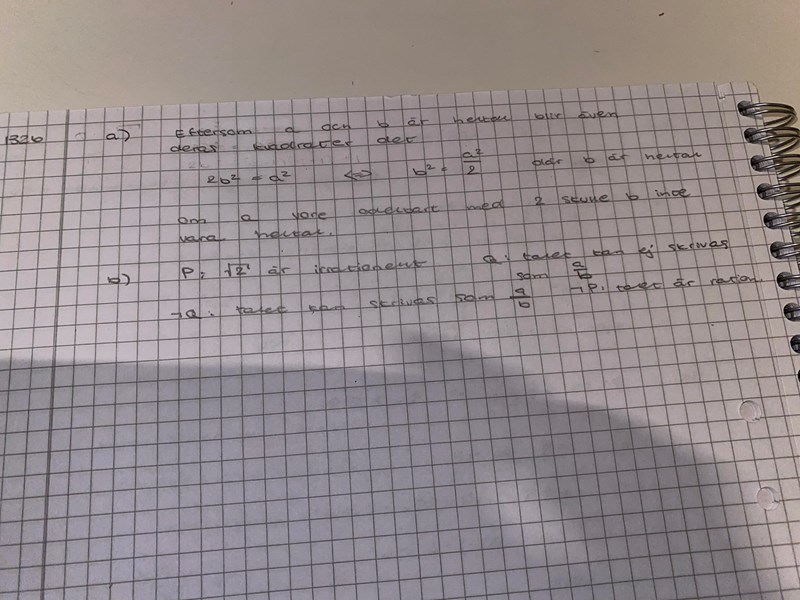
Jo, en motsägelse till det indirekta beviset är ”talet kan skrivas som a/b och talet är irrationellt”, vilket direkt ger en motsägelse, men jag vet inte om det är rätt väg att gå. Hur bör man generellt tänka i dessa fall, jag har lite svårt med bevis-processerna...

Hej,

Nyckeln till beviset är frasen "där kvoten a/b är förkortad så långt det går."

Resonemanget visar sedan att det går att förkorta kvoten $a/b$ ytterligare -- både $a$ och $b$ visar sig vara jämna tal -- vilket inte är möjligt om kvoten $a/b$ redan är förkortad så långt det går.

Albiki skrev:

Hej,

Nyckeln till beviset är frasen "där kvoten a/b är förkortad så långt det går."

Resonemanget visar sedan att det går att förkorta kvoten $a/b$ ytterligare -- både $a$ och $b$ visar sig vara jämna tal -- vilket inte är möjligt om kvoten $a/b$ redan är förkortad så långt det går.

Okej! Tänkte på en sak till detta. Man benämner ofta heltal som 2k, vilket jag vill ha bestämt för mig innebär en delbarhet med 2. Alla heltal är ju inte delbara med 2 (alla udda till exempel). Vad mer exakt menas med 2k? Hur kan jag använda detta?

Vad menar du med att det är delbart med 2? Om a eller b är ett udda tal blir ju dess kvadrat udda?

Upp

Om k är ett heltal (vilket som helst) så är 2k ett jämnt heltal.

2k - 1 (eller 2k +1) är då ett udda heltal. 

tindra03 skrev:

Albiki skrev:

Hej,

Nyckeln till beviset är frasen "där kvoten a/b är förkortad så långt det går."

Resonemanget visar sedan att det går att förkorta kvoten $a/b$ ytterligare -- både $a$ och $b$ visar sig vara jämna tal -- vilket inte är möjligt om kvoten $a/b$ redan är förkortad så långt det går.

Okej! Tänkte på en sak till detta. Man benämner ofta heltal som 2k, vilket jag vill ha bestämt för mig innebär en delbarhet med 2. Alla heltal är ju inte delbara med 2 (alla udda till exempel). Vad mer exakt menas med 2k? Hur kan jag använda detta?

 

Vad menar du med att det är delbart med 2? Om a eller b är ett udda tal blir ju dess kvadrat udda?

Nej, det är fel att heltal ofta benämns $2k$; det är endast jämna heltal som uttrycks på det sättet.