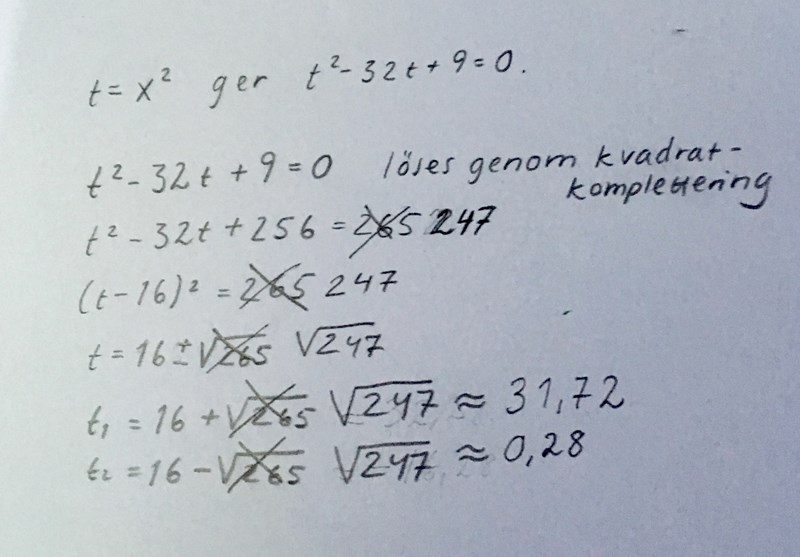Bevisa att ekvationen inte har några heltalslösningar
Jag har polynomekvationen
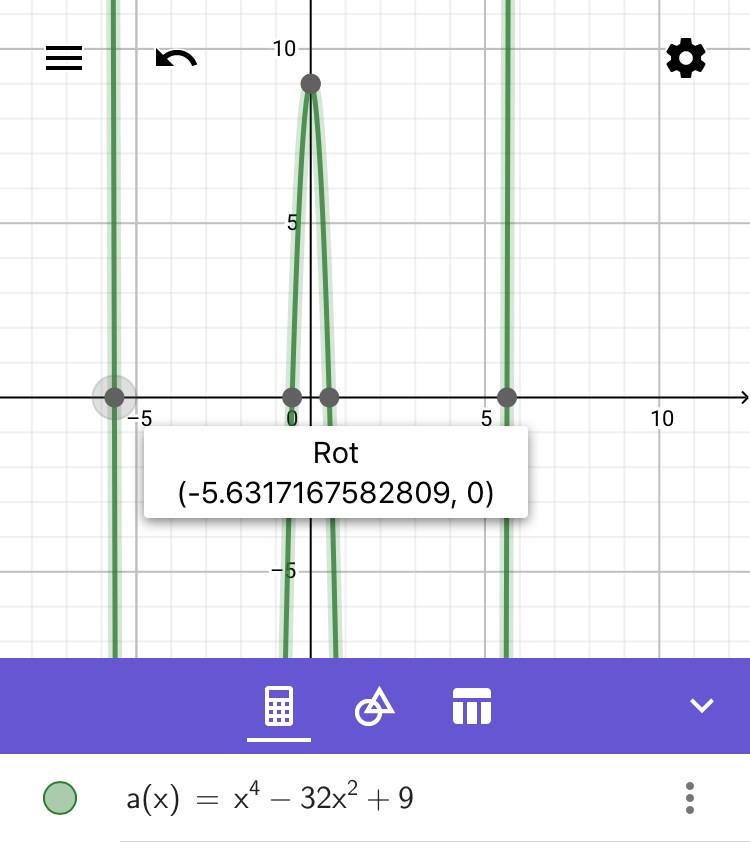
x^4-32x^2+9=0
och ska finna heltalslösningar. Jag misstänker att det inte finns några heltalslösningar (efter att ha testat med flera heltal).
Hur kan jag bevisa att inga heltalslösningar finns till ekvationen?
Du kan försöka lösa ekvationen och se vad x blir.
Gör substitutionen . Då får du en andragradsekvation.
Ja, det är klart jag ska göra en substitution.
Du ska inte byta tecken på nian. 256 - 9 = 247.
Nu har jag rättat felen.
Lisa Mårtensson skrev:Nu har jag rättat felen.
OK bra.
Nu återstår bara att substituera tillbaka till x och visa att lösningarna inte är heltal.
Verkar detta rimligt?
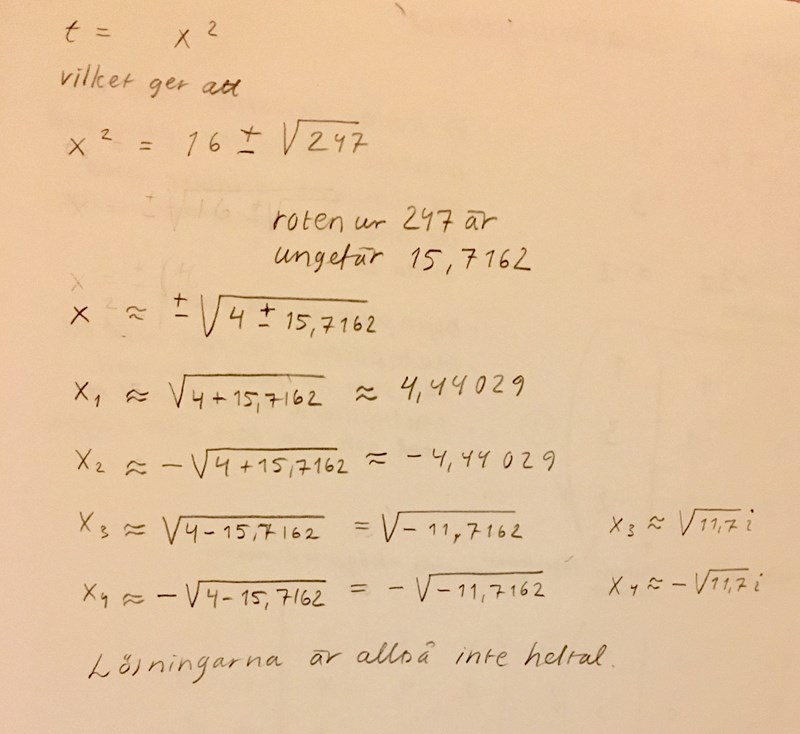
Lisa Mårtensson skrev:Verkar detta rimligt?
Nej det stämmer inte.
Om så är .
Om nu så är
Detta är inte samma sak som det du har skrivit.
Rationella rotsatsen säger att de enda heltalen som kan vara lösningar är delarna till 9, dvs -1,-3,-9, 1, 3, 9
Har man kontrollerat de 6 talen så har man uteslutit alla heltal.
Nej, jag ser ju att jag gjort helt fel. Ärligt talat skrev jag så som du skriver först. Det är ju tydligt att det ska vara så.
Räcker det som du skrev för att visa att det inte finns några heltslslösningar eller tycker du att man ska presentera alla fyra lösningarna?
Lisa Mårtensson skrev:Nej, jag ser ju att jag gjort helt fel. Ärligt talat skrev jag så som du skriver först. Det är ju tydligt att det ska vara så.
Räcker det som du skrev för att visa att det inte finns några heltslslösningar eller tycker du att man ska presentera alla fyra lösningarna?
Presentera alla fyra. Men det räcker med närmevärden.
Länk till rationella rotsatsen:
https://www2.math.su.se/~joeb/public/algokomb/extra/rationellarotter.pdf
q måste vara 1 eller -1. p måste vara 1, -1, 3, -3, 9, eller -9.
Hej!
En kvadratkomplettering av andragradspolynomet i ger polynomet
Detta är lika med noll för tal som uppfyller
Detta visar att kan inte vara ett jämnt tal eftersom 13 och 19 är inte delbara med 16. Den enda återstående möjligheten för att vara heltal är om är ett udda tal, men inte heller detta är möjligt eftersom då är inte delbart med varken 13 eller med 19 då det kan skrivas som där är ett heltal.
Bra förklarat Albiki, jag hänger med :-)
Lösningarna är att x är ungefär:
-5,632
-0,533
0,533
5,632
Bild av grafens nollställen, det aktuella fjärdegradspolynomets rötter: