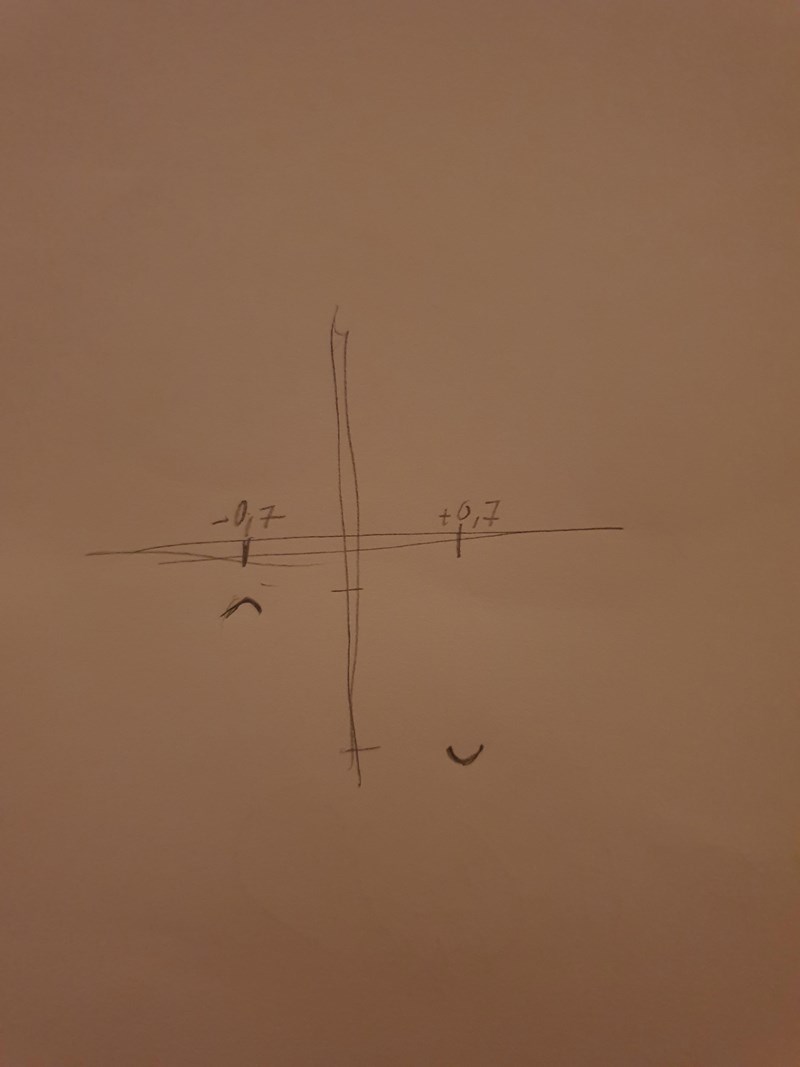Bevisa att en ekvation bara har en rot i ett visst intervall
Behöver hjälp med denna uppgiften. Förstår inte hur derivatan hjälper mig bevisa att det bara finns en rot. För deriverar jag funktionen och sätter derivatan till noll får jag fram att inom de angivna intervallet finns två extrempunkter. Hur går jag vidare? Tacksam för hjälp. 
Börja med att rita upp funktionen: för det givna intervallet:
Ja men om jag ritar upp den ser jag att där bara är en rot i intervallet. Men om jag inte går använda digitala hjälpmedel utan ska ta hjälp av derivatan hur gör jag då?
Deriverar. Ta reda på extrempunkterna och vad f(x) har för värde där.
Ja men det har jag gjort men vad ger det mig?
Vad har f(x) för värde på dina extrempunkter?
- 0.785 och +0.785. Är fortfarande inte med på hur det hjälper mig?
Kan du rita in det vi har kommit fram till i ett diagram? Det behöver inte vara exakt.
Där är extrempunkterna, hur går jag vidare?
Nu kan man hävda att det bara kan finnas en rot, eller hur?
Men hur vet jag att roten är i just det intervallet?
1. Är funktionen kontinuerlig i intervallet med de båda kända y-värdena?
2. Är derivatan antingen positiv i hela intervallet eller negativ i hela intervallet?
3. Är det ena y-värdet positivt och det andra negativt?
I så fall finns det exakt en nollpunkt mellan de kända värdena.
messi99 skrev:Men hur vet jag att roten är i just det intervallet?
Bra invändning. Du får räkna ut också.
Nu fattar jag! Tack igen! :)