Bevisa att k-reguljära bipartita grafer har kompletta matchningar

Hej!

Jag har följande uppgift:

"Om $G$ är $k$ -reguljär och bipartit, har $G$ en komplett matchning?"

Jag har tillgång till följande (kortfattade) facit:

Eftersom $\chi'(G)=\Delta(G)$ för k-reguljära bipartita grafer, så vet vi att alla "kantfärger" används för varje nod. Därför kan vi välja vilken av de utgående färgerna som helst (och kommer få en komplett matchning).

Jag vet vad Halls sats är, så ett alternativ hade kunnat vara att bevisa att $|N(S)|\ge |S|$ för alla delmängder $S$ till $X$ där $G=(X \cup Y$, E), X \cap Y = \emptyset$ .

Jag har letat efter lite bevis på nätet, nedan är ett exempel från https://math.stackexchange.com/questions/1805181/prove-that-a-k-regular-bipartite-graph-has-a-perfect-matching

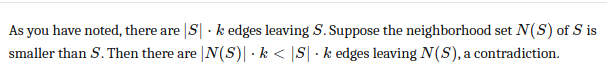
Jag tolkar ovanstående bevis så att det ska vara självklart att oavsett vilken delmängd $S$ som vi väljer ut, så vet vi att det inte finns två noder i $S$ som har en kant till samma nod i $N(S)$ . Detsamma problematik när jag läser det facit ovan som använder sig av kantfärger. Visst kan vi färga en kant per nod i $X$ olika färger, men hur kan vi utifrån det vara så säker att dessa kanter går till strikt olika noder i $Y$ ? ( $X \cup Y$ utgör den noderna i den bipartita grafen)

Om jag inte misstar mig så kan två noder i $S$ absolut ha kanter till samma nod i $N(S)$ . Däremot gäller följande:

Antalet utgående kanter från $S$ är $k|S|$ eftersom grafen är $k$ -reguljär. Alla dessa kanter går till något hörn i $N(S)$ .

Antalet utgående kanter från $N(S)$ är likaså $k|N(S)|$ .

Var och en av de $k|S|$ kanter som går från $S$ till $N(S)$ går även åt andra hållet från $N(S)$ till $S$ , så länge vi handskas med oriktade grafer. Alla kanter som går från $S$ till $N(S)$ ingår därför i mängden kanter som går ut från $N(S)$ .

Det betyder att $k|S|$ omöjligen kan vara större än $k|N(S)|$ .

Däremot kan $N(S)$ ha andra kanter som går mellan $N(S)$ och något hörn i $X\setminus S$ .

Så $k|S| \leq k|N(S)|$ vilket betyder att $|S|\leq |N(S)|$ , och villkoret för Halls sats är uppfyllt.

hur kan vi utifrån det vara så säker att dessa kanter går till strikt olika noder i $Y$ ?

En färgning av kanterna i grafen är alltid sådan att två kanter av samma färg aldrig har ett hörn gemensamt. Annars skulle vi kunna färga alla grafer med endast en färg. Givet att $G$ har en sådan färgning, så kan vi välja en av färgerna. Argumentet är då att eftersom den färgen (liksom alla andra) måste användas för varje nod, så kommer kanterna vi valt att täcka in alla hörn i grafen. Det ger oss en komplett matchning.

Tillägg: 9 sep 2025 13:53

Enklare sätt att tänka kring det första resonemanget: Om t.ex. $k=3$ och $|S|=5$ så går det 15 kanter ut från $S$ . Dessa kan omöjligen gå till färre än 5 hörn i $N(S)$ , eftersom då skulle något hörn i $N(S)$ ha grad högre än 3, vilket motsäger att grafen är 3-reguljär. Vi drar slutsatsen att $N(S)$ har minst lika många hörn som $S$ .

Svara