Bevisa att n^3-n är alltid delbart med 6

Om $n$ är udda, vi sätter $n=2k-1$ med $k=0,1,2...$ och så vidare.

${(2 k - 1)}^{3} - (2 k - 1) = 8 k^{3} - 12 k^{2} + 6 k - 1 - 2 k + 1 * h ä r h a r j a g f ö r s ö k t a t t P a s c a l t r i a n g u l e r a s a k e n m e n d e t g i c k i n t e, v a r f ö r ? = 8 k^{3} - 12 k^{2} + 6 k - 1 - 2 k + 1 = 8 k^{3} - 12 k^{2} + 4 k$

Men k är jämt så jag ersätter $k=2p$

$8 {(2 p)}^{3} - 12 {(2 p)}^{2} + 4 (2 p) = 8 * 8 p^{3} - 12 * 4 p^{2} + 4 * 2 * 2 p = 64 p^{3} - 12 * 4 p^{2} + 16 p$

Bara 12 är delbar med 6...

Jag vet inte om bara ett matematiskt resonemang håller, men detta är också ett sätt att lösa uppgiften på:

Skriv om uttrycket:

$n^{3} - n = n (n^{2} - 1) = n (n - 1) (n + 1)$ .

Ordna i storleksordning för att se beviset lättare:

$(n - 1) \cdot n \cdot (n + 1)$

Eftersom n är udda måste (n - 1) och (n + 1) vara jämna, vilket innebär att de innehåller två stycken faktor två. Hittills har vi bevisat att vårt uttryck är delbart med $2 \cdot 2$ . Men $24 = 2^{3} \cdot 3$ , så vi behöver hitta en faktor två till, och en faktor tre.

Vi har tre tal på rad, och därmed måste ett vara delbart med tre, vilket innebär att den innehåller en faktor tre vi kan bryta ut.

Delbarhet med två efter att vi brutit ut våra tvåor i ovanstående stycken är svårare. Vi letar egentligen efter delbarhet med fyra, eftersom endast dessa tal är jämna när vi dividerat en gång med två. Då ser tallinjen ut såhär:

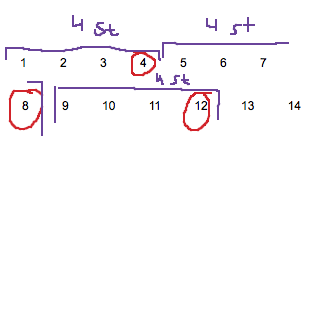
Vartannat jämnt tal, dvs. var fjärde heltal, är delbart med fyra. Vår stege innehåller endast tre tal. Vi kan därför inte allmänt säga att det finns ett tal som är delbart med fyra i vår talföljd. MEN! Vi vet att talet n är udda, och därmed måste vara omringat av två jämna tal som ingår i beräkningen. Eftersom vi sa att vartannat jämnt tal är delbart med fyra, har vi nu en garanti för att ett av talen, (n - 1) eller (n + 1) är delbart med fyra, och således innehåller två stycken faktor två (en har vi redan tagit). Vi kan då bryta ut vår sista tvåa, och vi har delbarhet med 24!

Tack Smutstvätt!

Jag är med tills delbarheten med två stycken 2 och en styck tre, så jag ska processa lite till!

Svara