Binomialfördelad sannolikhet
Har fastnat på en beräkning. Till min hjälp har jag jag en tabell.
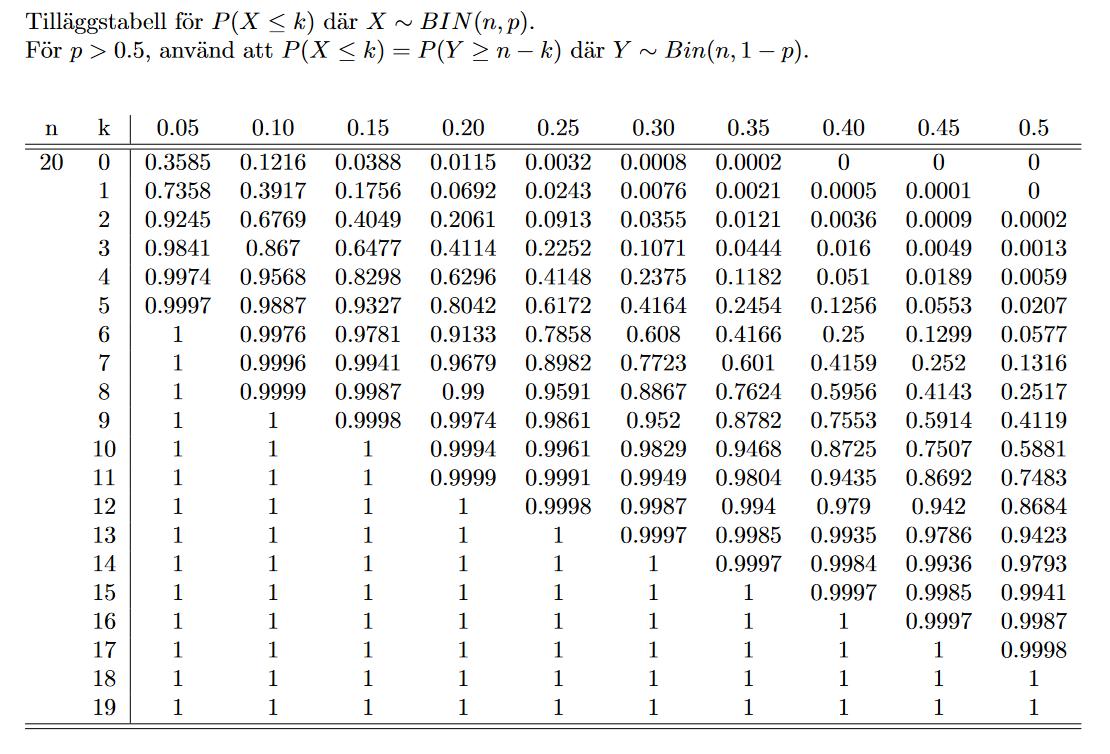
Jag har n = 20, k = 17.. 20 och p = 0.8
0.8 > 0.5 så måste vända på uttrycket.
Vill undersöka .
När jag vänder på uttrycket tänker jag att man bör få n = 20, k = 0,1,2,3 och p = 0.2 och därefter att man räknar men detta ger fel värde.
Kan man inte vända på uttrycket såhär?
Rätt svar är 0.4114, vilket är det värde P(Y=3) har. Varför tas ej k = 0,1,2 med?
Antingen är din uppgift felaktig eller så har du tolkat den felaktigt.
Upg:

"åtminstone"
Då har du tänkt rätt. Svaret är inte 0.4114
Hittade en given lösning till uppgiften, som verkar antyda på "åtminstone" men de gör inte omvandlingen?
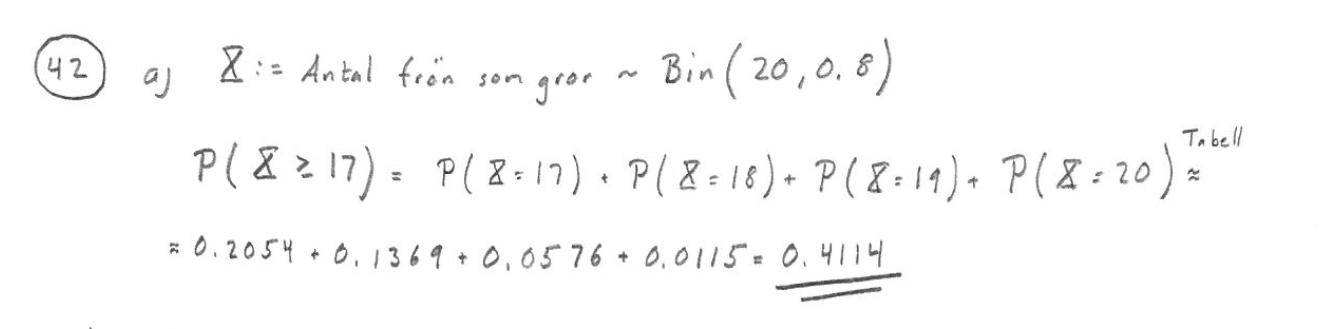
Jo, men man har inte skrivit ut att
Sannolikhet att 19 gror = Sannolikhet att 1 inte gror.
Aha, så det är fel i facit och min metod var korrekt?
Ja, det tycker jag.

