Bisektionsalgoritm
Hjälp! Jag fattar inget här.
Försökte lösa fråga 1 i avsnitt 2.2 . Man ska lösa f(x)=y där y=5 .
I uppgiften de har själva get f till f=@(x) x.^2 +x och y=5. Jag ersatt f med 5 och skrev g=x.^2+x-5
Och försökte anropa funktinget men det gick inte=((
En bisections funktion tar alltid en f, en I(gränserna) och en TOL. Jag har skrivit funktionen f(x)= x^2+x i själva koden och i commando fönstret skrev jag en en anonym funktion alltså g= @(x)f(x) -5 och det skapades en plats för det i min workspace(vet ej om jag har gjort rätt)
Några saker som jag har inte förstått: Varför det går inte att anropa funktionen genom att skriva [x] = bisection2(g, [1 2], 10^(-9) ) ?? Hur vet man mellan vilken intervall man ska leta efter något?? Läste att man ska rita grafen först för att see hur den ser ut och kunna veta ungefär var lösningen ligger. Men om hur ska man platta något när man inte vet något om x och y axlarna??? I funktionen står det att den tar en I alltså gränsvärde men hur vet man vilka gränsvärde man ska skicka??
Vad jag skrev:
I am Me skrev:Hjälp! Jag fattar inget här.
Försökte lösa fråga 1 i avsnitt 2.2 . Man ska lösa f(x)=y där y=5 .
I uppgiften de har själva get f till f=@(x) x.^2 +x och y=5. Jag ersatt f med 5 och skrev g=x.^2+x-5
Och försökte anropa funktinget men det gick inte=((
En bisections funktion tar alltid en f, en I(gränserna) och en TOL. Jag har skrivit funktionen f(x)= x^2+x i själva koden och i commando fönstret skrev jag en en anonym funktion alltså g= @(x)f(x) -5 och det skapades en plats för det i min workspace(vet ej om jag har gjort rätt)
Några saker som jag har inte förstått: Varför det går inte att anropa funktionen genom att skriva [x] = bisectionsrot(g, [1 2], 10^(-9) ) ?? Hur vet man mellan vilken intervall man ska leta efter något?? Läste att man ska rita grafen först för att see hur den ser ut och kunna veta ungefär var lösningen ligger. Men om hur ska man platta något när man inte vet något om x och y axlarna??? I funktionen står det att den tar en I alltså gränsvärde men hur vet man vilka gränsvärde man ska skicka??
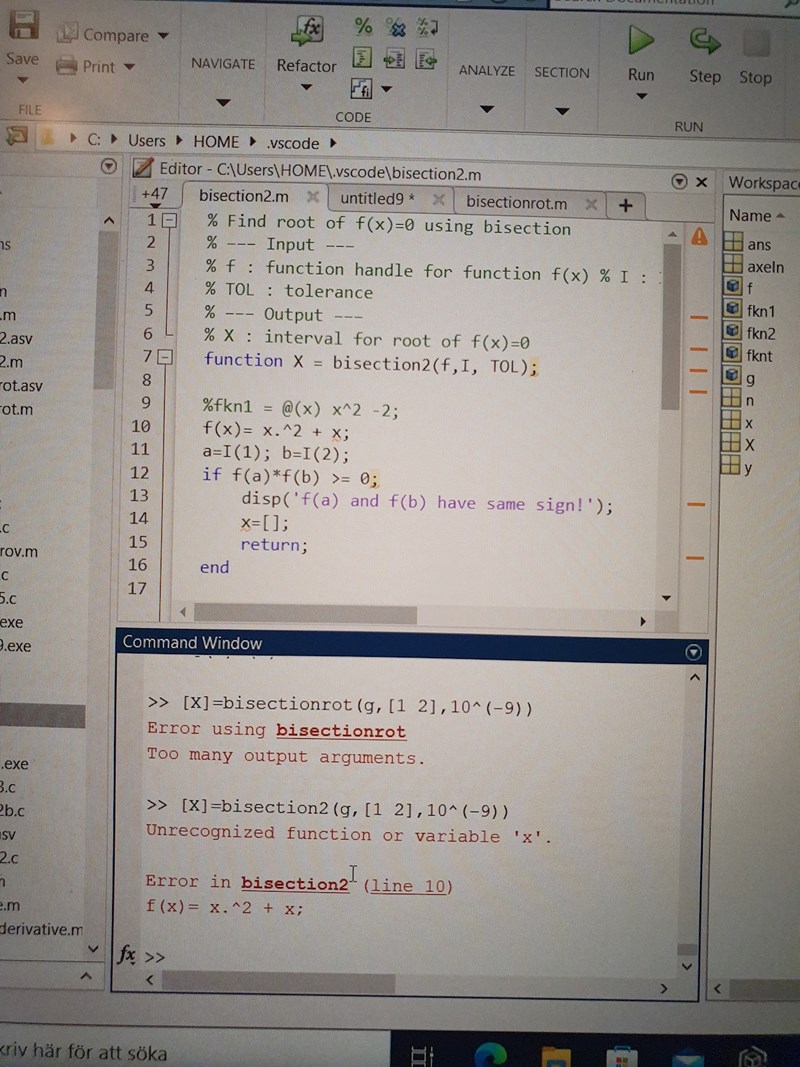
Vad jag skrev:
En sak till. När jag skriver min funktion så har jag skrivit att det som ska skrivas ut är X alltså function X=bisections2(f, I, TOL) men varför behöver jag i anropet skriva hackprantser runt X ???
Mycket konstigt här...
I rad 7 tar du f som ett inargument, dvs. du vill skicka ett funktionshandtag till funktionen.
Sedan försöker du definiera f på rad 10... men 1) f är ett inargument 2) f(x) innebär indexering av en vektor med indexen x.
Tanken är nog att utanför funktionen definiera f, t.ex "f=@(x) x.^2 +x" och skicka f till bisection2.
Börja med att fixa till det.
Sista frågan, du behöver inte sätta hakparenteser i det fallet. Om funktionen returnerar flera variabler så skall du ha hakparenteser om du vill ta vara på alla, annars får du bara den första.
Matsmats skrev:Mycket konstigt här...
I rad 7 tar du f som ett inargument, dvs. du vill skicka ett funktionshandtag till funktionen.
Sedan försöker du definiera f på rad 10... men 1) f är ett inargument 2) f(x) innebär indexering av en vektor med indexen x.
Tanken är nog att utanför funktionen definiera f, t.ex "f=@(x) x.^2 +x" och skicka f till bisection2.
Börja med att fixa till det.
Sista frågan, du behöver inte sätta hakparenteser i det fallet. Om funktionen returnerar flera variabler så skall du ha hakparenteser om du vill ta vara på alla, annars får du bara den första.
"Sedan försöker du definiera f på rad 10... men 1) f är ett inargument 2) f(x) innebär indexering av en vektor med indexen x."
Förstår inte vad du menar här
Jag börjar hata matlab!:( fastnar i varenda uppgift och tar så mycket tid.
Det fungerar fortfarande inte. I texten under rubriken "Inversa funktioner" står det att man ska först skriva sin funktion i formen ax^2 + bx + c=0 och sedan hitta funktionens nollställe då kan man räkna rötterna/ roten med bisactions algoritmen.
Aha ok, så man måste definiera en funktion utanför för att man har skrivit att bisection2 funktionen tar ett f så därför måste f vara utanför koden?
Ja, det var det jag menade med att du tar f som inargument till funktionen men sedan försöker definiera f(x) på rad 10.
Så precis som du skriver, du skall definiera en funktion utanför, t.ex. med f=@(x) x.^2+b*x+c
En grej jag tycker man missar i undervisningen är att lära sig debug med hjälp av brytpunkter. Det finns en hel del material på webben om man söker på MATLAB debug, dock på engelska. Om du vill ha en bra MATLAB-handledning på svenska så kan du hitta begagnade exemplar av "Användarhandledning för MATLAB" av Eva Pärt-Enander och Anders Sjöberg. Ligger nästan alltid på mitt skrivbord. Den täcker tyvärr inte in modernare versioner men mycket av det du håller på med.


