Blandningsproblem
Två behållare, A och B, läcker ut salthaltigt vatten med en hastighet 10 L/min respektive 5 L/min i en behållare C som ursprungligen innehöll 100 L rent vatten. Volymprocenten salt i A är 4% och i B 10%. Det rinner samtidigt ut vatten ur C in i en behållare D (som också ursprungligen hade 100 L rent vatten) med hastigheten 15 L/min. Ur D rinner det 10 L/min. Bestäm volymprocenten salt i behållare D efter 10 minuter.
apple8 skrev:
Jag har inte kollat din beräkning, men frågan är
Bestäm volymprocenten salt i behållare D efter 10 minuter.
så 3.36 L är inte svaret på frågan.
Menar man med volymprocent, andelen salt i blandningen för då tänkte jag dela med 100
Jag har inte facit till frågan och vill veta ifall jag tänker rätt
Är detta en analytisk uppgift eller numerisk med hjälp av digitala verktyg mm?
Om jag inte missar något så verkar den överdrivet svår analytiskt.
Jag antar att man får använda digitala verktyg
apple8 skrev:Jag antar att man får använda digitala verktyg
Hur pass kraftiga?
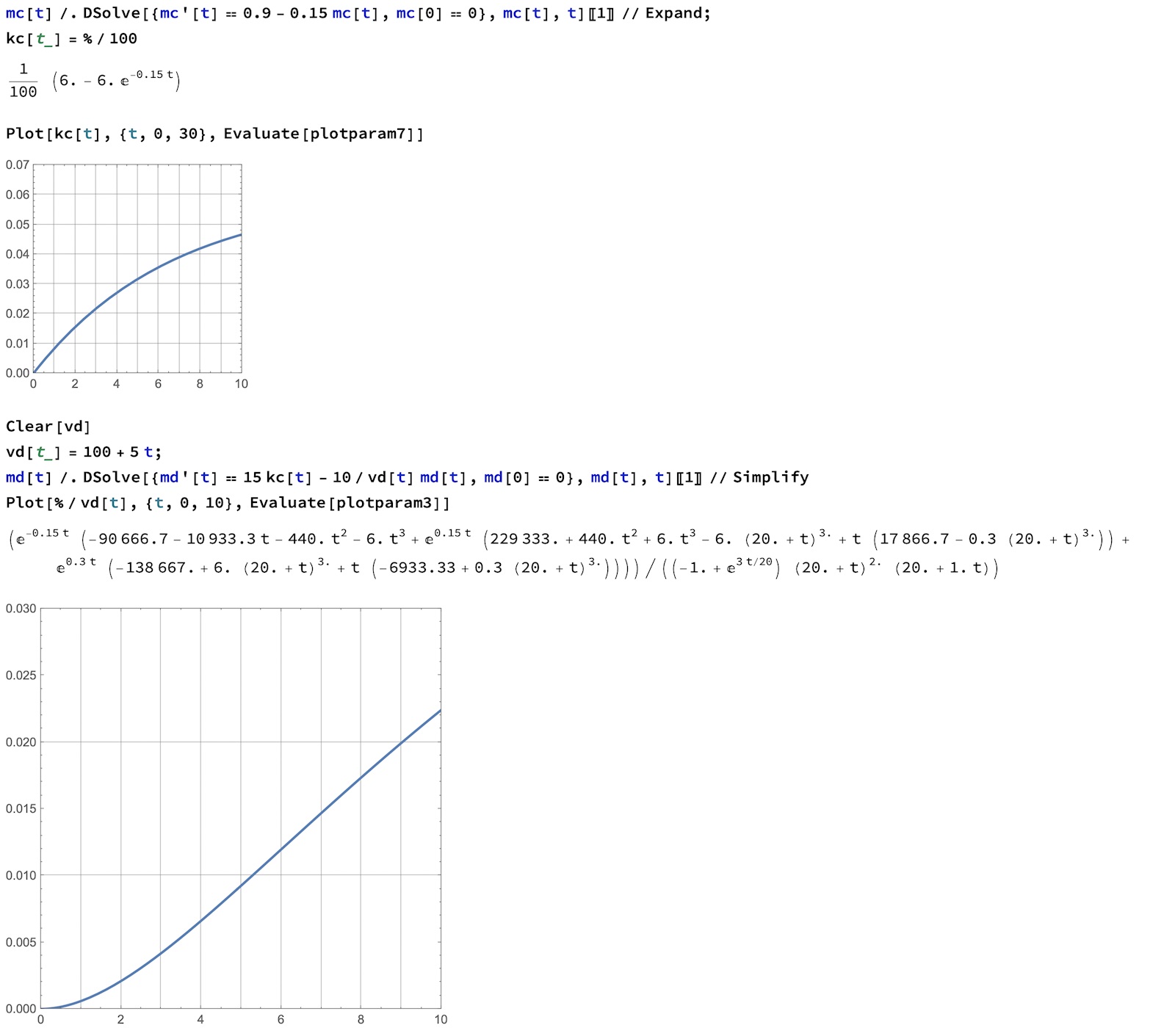
Jag ser det som en 2-stegs-process. Först gäller det att finna ett uttryck för konc. i behållare C och sedan därefter skapa en ny diff.ekv. för behållare D. Den sista blir inte rolig, men Mathematica knäcker den lätt. Frågan är vilka verktyg boken har i tanke.
Jag hittade uppgiften på nätet så jag vet inte riktigt men vad får du för svar med Mathematica
0.0224154
Vad säger facit?
Rätt svar, det jag inte tog hänsyn var att volymen förändras så man delar inte med 100 utan med 150(Volym efter 10 min)
apple8 skrev:Rätt svar, det jag inte tog hänsyn var att volymen förändras så man delar inte med 100 utan med 150(Volym efter 10 min)
Det är nog lite knepigare än så men det kan vara att siffrorna är så små och grafen så flack att det spelar ingen roll att man uppskattar det med en linjär funktion.
Ja, den är nästan linjär så man kan nog göra en uppskattning som du gjort
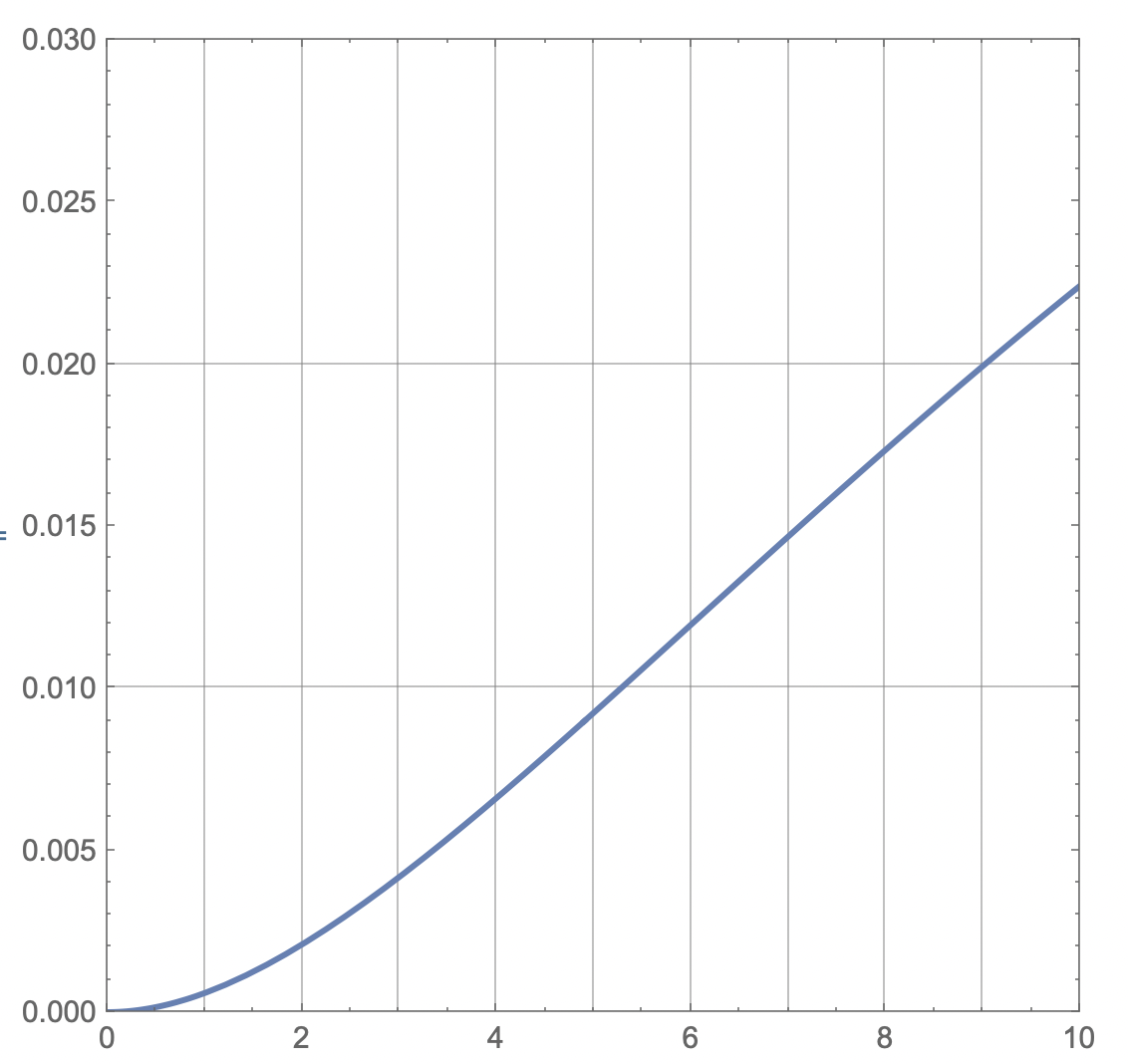
Dock är det ej sant för större t-värden

Så här ser det ut när MMA löser ekvationen som är långt över någon vanlig kurs i diff.ekv.