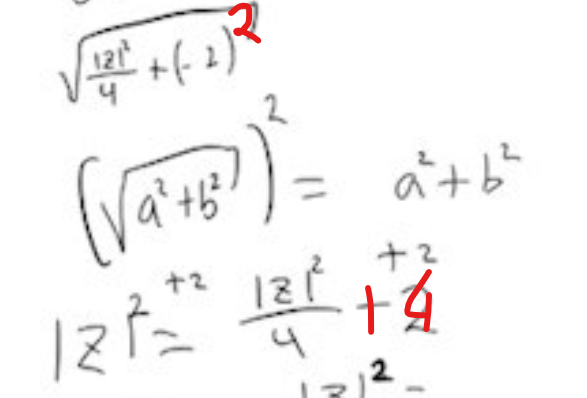Blev detta heltokigt?

anta att z = a+bi så blir din ekvation,

$a^2+b^2 = 4a +4bi +8i$

separera real och imaginärdel

ekv 1: 4b +8 = 0  (imaginärdelen)

ekv 2:  a²+b² = 4a (realdelen)

ur ekv 1 får vi att b = -2

a kanske du kan lösa ut själv med hjälp av ekv 2?

Om jag läser rätt:

Någonstans mitt i dina beräkningar har du råkat skriva att b^2 är -2, och sedan blir det lite följdfel med negativa absolutbelopp 

Tures lösning är mycket enklare. 

Simonload10 skrev:

Man ska lösa ekvationen ${\left|z\right|}^2=4z+8i$

Det var en intressant (dock ovanlig) lösningsmetod, men den borde faktiskt fungera.

Du har kommit fram till att b=-2.

Du har helt rätt skrivit att $|z| = \sqrt{a^2 + b^2}$ och sedan har du tecknat ekvationen $a = \dfrac{|z|^2}{4}$. Den ekvationen har du dock inte löst! Gör det!

$a = \dfrac{|z|^2}{4}$ är ekvivalent med att $a = \dfrac{a^2 + b^2}{4}$.

Eftersom man redan vet att $b=-2$, så är $a = \dfrac{a^2 + (-2)^2}{4}$ och därmed $a = \dfrac{a^2}{4} + 1$

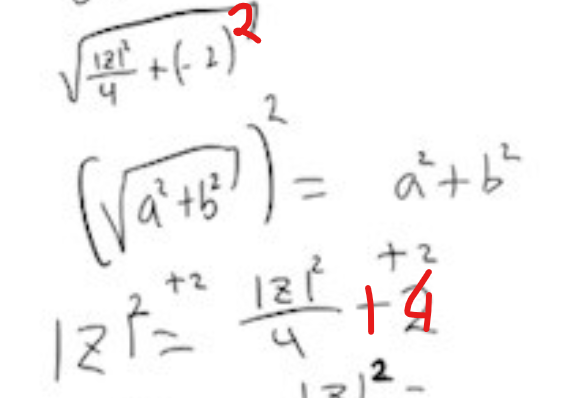
Ture skrev:

anta att z = a+bi så blir din ekvation,

$a^2+b^2 = 4a +4bi +8i$

separera real och imaginärdel

ekv 1: 4b +8 = 0  (imaginärdelen)

ekv 2:  a²+b² = 4a (realdelen)

ur ekv 1 får vi att b = -2

a kanske du kan lösa ut själv med hjälp av ekv 2?

Hur kan högerledet bli $4a+4bi+8i$?

LuMa07 skrev:

Simonload10 skrev:

Man ska lösa ekvationen ${\left|z\right|}^2=4z+8i$

Det var en intressant (dock ovanlig) lösningsmetod, men den borde faktiskt fungera.

Du har kommit fram till att b=-2.

Du har helt rätt skrivit att $|z| = \sqrt{a^2 + b^2}$ och sedan har du tecknat ekvationen $a = \dfrac{|z|^2}{4}$. Den ekvationen har du dock inte löst! Gör det!

$a = \dfrac{|z|^2}{4}$ är ekvivalent med att $a = \dfrac{a^2 + b^2}{4}$.

Eftersom man redan vet att $b=-2$, så är $a = \dfrac{a^2 + (-2)^2}{4}$ och därmed $a = \dfrac{a^2}{4} + 1$

---

Fel i ursprungliga uträkningen

Som Bubo redan poängterat, så blev din ursprungliga uträkning fel på följande rader

Varför ska endast andra termen i rottecknet vara upphöjt till 2? I min beräkning var det ju isåfall fel att inte båda termerna var upphöjda till två? Skrev du 14 istället för -2? alltså +14?

Simonload10 skrev:

Varför ska endast andra termen i rottecknet vara upphöjt till 2? I min beräkning var det ju isåfall fel att inte båda termerna var upphöjda till två? Skrev du 14 istället för -2? alltså +14?

Nej, det är inte endast andra termen som ska vara upphöjt till 2. Jag glömde att markera den första termen också. Den borde också ha varit upphöjt till 2. (Detta påverkar förstås även raden längre ner.)

Jag skrev inte +14, utan +4 (då jag strök över minustecknet för att göra det till ett plustecken och sedan 2:an ändrades till 4:an)

LuMa07 skrev:

Simonload10 skrev:

Varför ska endast andra termen i rottecknet vara upphöjt till 2? I min beräkning var det ju isåfall fel att inte båda termerna var upphöjda till två? Skrev du 14 istället för -2? alltså +14?

Nej, det är inte endast andra termen som ska vara upphöjt till 2. Jag glömde att markera den första termen också. Den borde också ha varit upphöjt till 2. (Detta påverkar förstås även raden längre ner.)

Jag skrev inte +14, utan +4 (då jag strök över minustecknet för att göra det till ett plustecken och sedan 2:an ändrades till 4:an)

Stort tack