Blir det samma svar?
På denna lösningen använde han en punkt som ligger på den possitiav delen av x och y koordinaterna, första kvadraten. Därför blir sträckan PQ possivit och lika med RQ eftersom en stevka ALLTID är possivit men jag undrade ifall det hade ändå blivit possitiv om jag hade tagit en sticka från 4 kvadraten, då x och y värden är negativa.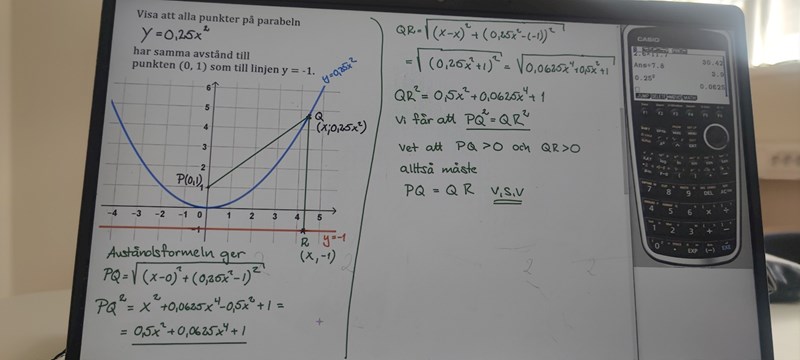
Prova!
Jo, det fungerar även om Q ligger till vänster om y-axeln (det är andra kvadranten, inte fjärde).
Om du har två punkter (a, b) och (c, d) var som helst i planet så kan avståndet mellan dem alltid skrivas roten ur [ (a–c)2 + (b–d)2 ]
Vi vet att (a–c)2 = (c–a)2 och att (b–d)2 = (d–b)2.
Ex Om a–c = 7 så är c–a = –7, och 72 = (–7)2
En kvadrat är alltid positiv (eller 0) så summan av två kvadrater kan inte vara negativ.
Roten ur x2 är x om x är positivt och –x om x är negativt, dvs roten ur x2 är aldrig negativ.

