Bordens ände Algebra
Det får plats x personer runt ett rektangulärt bord. Det kan sitta en person på varje kort- ända. Flera bord sätts ihop i kortändorna skriv förenklade uttryck för hur många personer som kan sitta runt
a) två bord
b)fyra bord
Hur ska man tänka?
Vore tacksam för hjälp mycket tacksam!? ;D
Försök rita en figur över hur det ser ut. Det bör man alltid göra.
HT-Borås skrev:Försök rita en figur över hur det ser ut. Det bör man alltid göra.
Mhm okej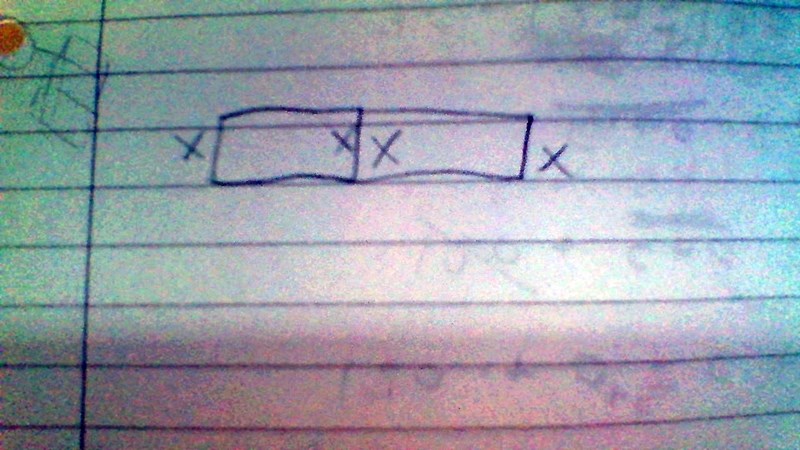 Oki doki har ritat jag vet att det kan sitta en pers på varje ände och om man sätter ihop borden så går det ju inte alltså dom personerna som sitter vid änden kallar jag två ex och dom i mitten som inta kan längre sitta där kallar jag för 2 så 2x-2?
Oki doki har ritat jag vet att det kan sitta en pers på varje ände och om man sätter ihop borden så går det ju inte alltså dom personerna som sitter vid änden kallar jag två ex och dom i mitten som inta kan längre sitta där kallar jag för 2 så 2x-2?
NanobotsLevelA skrev:HT-Borås skrev:Försök rita en figur över hur det ser ut. Det bör man alltid göra.
Mhm okej
Oki doki har ritat jag vet att det kan sitta en pers på varje ände och om man sätter ihop borden så går det ju inte alltså dom personerna som sitter vid änden kallar jag två ex och dom i mitten som inta kan längre sitta där kallar jag för 2 så 2x-2?
Hjälp så många online varför kolar inga?
Alltså, på a) tycker jag att 2x-2 borde stämma om jag inte är helt virr nu...
På b) så tänker du hur många kortsidor som ingen kan sitta vid och subtraherar det från, i detta fall 4 stycken x.
nikoniko skrev:På b) så tänker du hur många kortsidor som ingen kan sitta vid och subtraherar det från, i detta fall 4 stycken x.
Ok så korts sidorna är 4x och dom långa är 6 alla sammanlagt tillsamman är det då 4x-6?...............
Ja, exakt! Då har du också löst b)!
nikoniko skrev:Ja, exakt! Då har du också löst b)!
Ok tack för hjälpen ;D <3
Om det kanske skulle stå t.ex. 8 bord så skulle du kunna räkna ut det på samma sätt.
X-antalet bord minus hur många personer som inte kan sitta vid de blockerade kortsidorna.
NanobotsLevelA skrev:nikoniko skrev:Ja, exakt! Då har du också löst b)!
Ok tack för hjälpen ;D <3
Varsågod, jag är glad att kunna få hjälpa någon!
nikoniko skrev:Om det kanske skulle stå t.ex. 8 bord så skulle du kunna räkna ut det på samma sätt.
X-antalet bord minus hur många personer som inte kan sitta vid de blockerade kortsidorna.
Ok ska försöka vänta ett tag...
NanobotsLevelA skrev:nikoniko skrev:Om det kanske skulle stå t.ex. 8 bord så skulle du kunna räkna ut det på samma sätt.
X-antalet bord minus hur många personer som inte kan sitta vid de blockerade kortsidorna.
Ok ska försöka vänta ett tag...
Um 8x-16
Du får tänka att det är 7 kortsidor blockerade, alltså 14 pers. som inte kan sitta där, då blir det 8x-14, men jag tror att det bara var ett slarvfel, händer alla ;).


-(1).jpg?width=80&crop=0,0,80,80)
