Brantast uppför resp. nedför i en riktning (gradient, flervariabelanalys)
Hej, jag skulle behöva lite hjälp med följande uppgift:
Berget Vretos i Grekland beskrivs i lämpliga enheter av
z=1/100(50−x^2−y^2), x^2+y^2≤50
Vid en vandring från byn Laros med koordinaterna (7,-1,0) till byn Didos med koordinaterna (-1,3,0,4) går man på en stig vars projektion på xy-planet är den räta linjen från (7,-1,0) till (-1,3,0). Var är det brantast uppför respektive nerför i stigens riktning och hur stora är lutningarna där? Fikapausen tar man lämpligen i den punkt där det är plant i stigens riktning. Var är det?
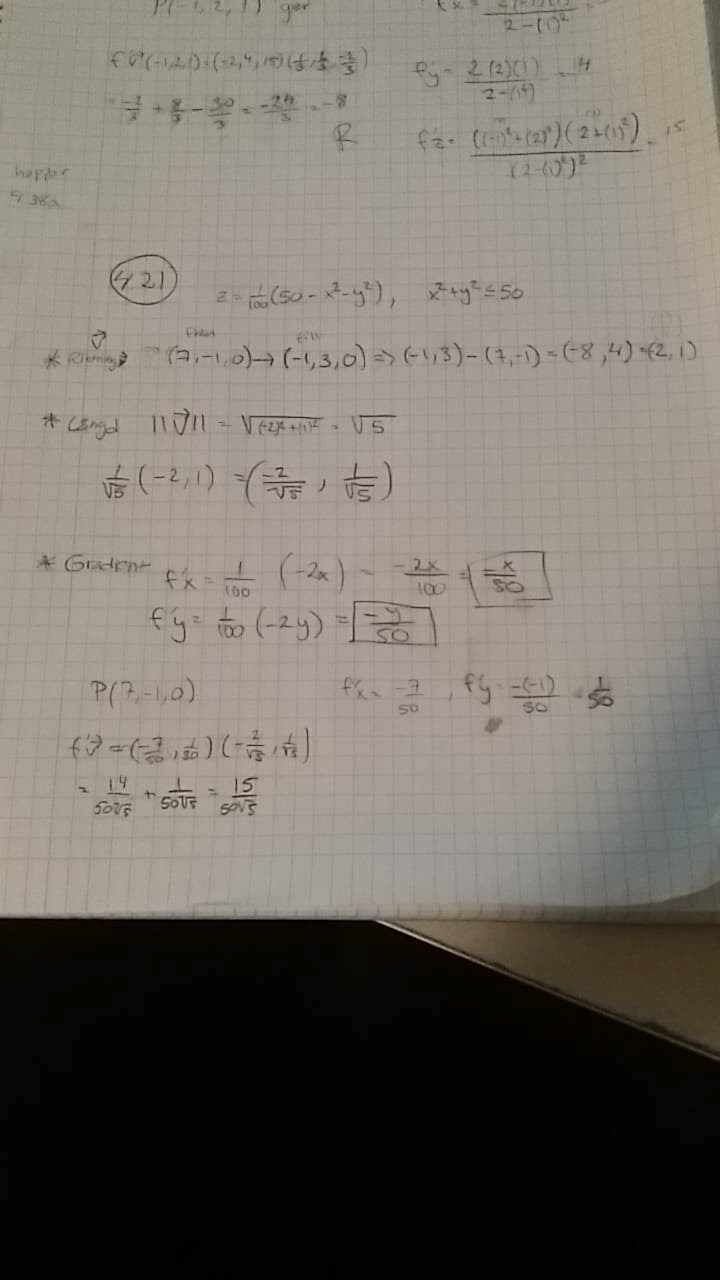
Som ni ser har jag tagit fram riktningsvektorn (-2,1)
- Vektorns längd sqrt(5) och normerat den 1/sqrt(5) * (-2,1) = (-2/sqrt(5), 1/(sqrt(5))
- tagit fram gradienterna f'x = -x/50, f'y = -y/50.
Därefter har jag räknat ut räknat ut riktningsderivatan i P(7,-1,0) vilket jag får till 15/50sqrt(5). Vet dock inte om jag ska göra det här. Svaret ska bli;
Max lutning: 3sqrt(5)/50
Min lutning: -sqrt(5)/50
fikapaus: P(1,2,0.45).
Hur de får fram dessa värden har jag inte en blekaste aning om.
Tänk på att när vi går på stigen kan x- och y-koordinaterna parametriseras som
(x, y) = (7, -1) + t(-8, 4), (0 t 1) (1).
Vi har riktningsderivatan i riktningen = enligt
= (2).
Vi kan nu sätta in parametriseringen av x och y enligt (1) i formeln för riktningsderivatan (2) och får då efter förenkling att
= (3).
Max erhålls då t = 0. Min då t = 1. Lutningen är noll då t = 3/4.
Resten klarar du själv.
PATENTERAMERA skrev:Tänk på att när vi går på stigen kan x- och y-koordinaterna parametriseras som
(x, y) = (7, -1) + t(-8, 4), (0 t 1) (1).
Vi har riktningsderivatan i riktningen = enligt
= (2).
Vi kan nu sätta in parametriseringen av x och y enligt (1) i formeln för riktningsderivatan (2) och får då efter förenkling att
= (3).
Max erhålls då t = 0. Min då t = 1. Lutningen är noll då t = 3/4.
Resten klarar du själv.
Jag har fått den generella riktningsderivatan
jag fattar inte det med parametriseringen för i min bok står det inte något om det. Efter den generella riktningsderivatan står det: "På stigen är x och y kopplade genom linjens ekvation så lutningen blir f'v = "
Jag förstår inte hur de får ifrån. Jag fattar att de löst ut y från någon formel och stoppat in i den generella riktningsderivatan och förenklat men vilken formel?
Sedan står det: "Denna avtar från ". Hur vet man detta? Och hur får man fram den slutgiltiga punkten där lutningen är 0? (dvs där de tar paus)".
Kovac skrev:... Efter den generella riktningsderivatan står det: "På stigen är x och y kopplade genom linjens ekvation så lutningen blir f'v = "
Jag förstår inte hur de får ifrån. Jag fattar att de löst ut y från någon formel och stoppat in i den generella riktningsderivatan och förenklat men vilken formel?
Det står i uppgiftstexten.
Vid en vandring från byn Laros med koordinaterna (7,-1,0) till byn Didos med koordinaterna (-1,3,0,4) går man på en stig vars projektion på xy-planet är den räta linjen från (7,-1,0) till (-1,3,0).
Vilken är funktionen för "den räta linjen från (7,-1,0) till (-1,3,0)"? Lös ut y som en funktion av x.
Smaragdalena skrev:Kovac skrev:... Efter den generella riktningsderivatan står det: "På stigen är x och y kopplade genom linjens ekvation så lutningen blir f'v = "
Jag förstår inte hur de får ifrån. Jag fattar att de löst ut y från någon formel och stoppat in i den generella riktningsderivatan och förenklat men vilken formel?
Det står i uppgiftstexten.
Vid en vandring från byn Laros med koordinaterna (7,-1,0) till byn Didos med koordinaterna (-1,3,0,4) går man på en stig vars projektion på xy-planet är den räta linjen från (7,-1,0) till (-1,3,0).
Vilken är funktionen för "den räta linjen från (7,-1,0) till (-1,3,0)"? Lös ut y som en funktion av x.
Då får jag 7x-y = -x+3y --> 8x = 4y --> y= 2x ?
Kovac skrev:Smaragdalena skrev:Kovac skrev:... Efter den generella riktningsderivatan står det: "På stigen är x och y kopplade genom linjens ekvation så lutningen blir f'v = "
Jag förstår inte hur de får ifrån. Jag fattar att de löst ut y från någon formel och stoppat in i den generella riktningsderivatan och förenklat men vilken formel?
Det står i uppgiftstexten.
Vid en vandring från byn Laros med koordinaterna (7,-1,0) till byn Didos med koordinaterna (-1,3,0,4) går man på en stig vars projektion på xy-planet är den räta linjen från (7,-1,0) till (-1,3,0).
Vilken är funktionen för "den räta linjen från (7,-1,0) till (-1,3,0)"? Lös ut y som en funktion av x.
Då får jag 7x-y = -x+3y --> 8x = 4y --> y= 2x ?
Jag vet inte vad din uträkning har för geometrisk tolkning, men en sak som ska gälla för linjen är att (7,-1) ska ligga på den, och 2*7 är inte -1.
Laguna skrev:Kovac skrev:Smaragdalena skrev:Kovac skrev:... Efter den generella riktningsderivatan står det: "På stigen är x och y kopplade genom linjens ekvation så lutningen blir f'v = "
Jag förstår inte hur de får ifrån. Jag fattar att de löst ut y från någon formel och stoppat in i den generella riktningsderivatan och förenklat men vilken formel?
Det står i uppgiftstexten.
Vid en vandring från byn Laros med koordinaterna (7,-1,0) till byn Didos med koordinaterna (-1,3,0,4) går man på en stig vars projektion på xy-planet är den räta linjen från (7,-1,0) till (-1,3,0).
Vilken är funktionen för "den räta linjen från (7,-1,0) till (-1,3,0)"? Lös ut y som en funktion av x.
Då får jag 7x-y = -x+3y --> 8x = 4y --> y= 2x ?
Jag vet inte vad din uträkning har för geometrisk tolkning, men en sak som ska gälla för linjen är att (7,-1) ska ligga på den, och 2*7 är inte -1.
Nej uppenbarligen fel så hur ska jag göra? Är det inte ett enkelt ekvationssystem man löser för att få ut y?
Gör som du lärde dig i Ma2: Du har punkterna ((7,-1) och (-1,3) (z-koordninaten saknar betydelse för den räta linjen eftersom vi tittar å en projektion i xy-planet). vilket ger . Sätt in k-värdet och koordinaterna från endera punkten i räta linjens ekvation y=kx+m så kan du beräkna att m = 2,5. Du har alltså y=2,5-0,5x eller y=½(5-x).
Det finns alltid flera sätt att parametrisera en kurva.
Jag valde ett sätt, som är relativt standardmässigt.
I den lösning som boken nämner så har man valt att se x som den oberoende variabeln och y som den beroende variabeln, och detta är ju också en vanlig form av parametrisering. Detta är ju bara en tillämpning av räta linjens ekvation från gymnasiet. Du har två punkter i x-y-planet. Använd tvåpunktsformeln för att ta fram räta linjens ekvation.
Vi kan även utgå från min parametrisering för att hitta den ekvation som används i boken.
Vi har som sagt följande parametrisering (en av många möjliga)
x = 7 - 8t
y = -1 + 4t
0 t 1
Vi kan nu istället välja x som oberoende parameter och lösa ut t som en funktion av x från den första ekvationen.
t = (7 - x)/8, där -1 x 7.
Vi kan nu sätta in detta uttryck för t i den andra ekvationen och får då efter förenkling att
y = (5 - x)/2.
Om vi sätter in detta uttryck i formeln för riktningsderivatan så får vi precis som boken säger att
= , men kom i håg mellan vilka värden x kan variera.
Uppenbarligen blir riktningsderivatan noll då x = 1. Riktningsderivatans största värde får man då x är så stort som möjligt (x = 7) och dess minsta värde då x är så litet som möjligt (x = -1).
Adams har en bra figur om riktningsderivata:
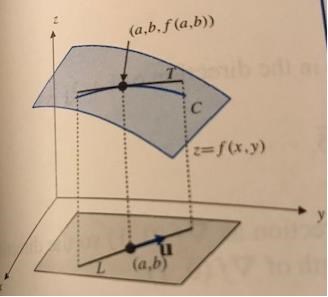
Stigens (L i figuren) projektion i xy-planet är viktig information för lösandet av uppgiften. Vi startar i punkten (7,-1) och slutar
i punkten (-1,3). PATENTERAMERA:s parameterframställning är elegant, men vi kan alternativt bestämma L:s ekvation (t ex med den välbekanta enpunktsformeln)
, varav . Överens?
Riktningsderivatan: , där
.
Gradienten
Allt detta ger . Sätt in , varav
.
Notera att i startpunkten (x=7) har vi största värdet på , medan i slutpunkten (x=-1) har vi minsta värdet på riktningsderivatan. då x=1. Då återstår att lösa ut sökta koordinaterna (x,y,z) ur denna information, det fixar du på egen hand, eller hur?
Återkoppla gärna!
dr_lund skrev:
Notera att i startpunkten (x=7) har vi största värdet på , medan i slutpunkten (x=-1) har vi minsta värdet på riktningsderivatan. då x=1. Då återstår att lösa ut sökta koordinaterna (x,y,z) ur denna information, det fixar du på egen hand, eller hur?
Återkoppla gärna!
Då är jag med. Lite frågor.
1. Är riktningsderivatans högsta värde = brantast lutning på stigen i detta fall? Samma med lägsta värdet? Hur vet jag vilken av de två lutningarna jag fått som är uppför resp. nedför? Har det med minustecknet framför att göra? Dvs lutningen är också den brantaste lutningen nedför i backens/linjens riktning pga minustecknet?
2. Varför gör man inget med koordinaterna från städerna? Kunde man inte använda de också?
3. Vi gjorde ju en förenkling av och räknade ut y med hjälp av de två punkterna som angavs och sedan stoppade in i formeln. Var man tvungen att göra såhär? Det går inte annars eller?
PATENTERAMERA skrev:
Då är jag med. Konstigt att man inte kan multicitera. Men mina frågor till Dr_Lund är riktade till dig också om du vill svara :)
Jag ska försöka besvara dina frågor.
1. Är riktningsderivatans högsta värde = brantast lutning på stigen i detta fall? Samma med lägsta värdet? Hur vet jag vilken av de två lutningarna jag fått som är uppför resp. nedför? Har det med minustecknet framför att göra? Dvs −5√50lutningen är också den brantaste lutningen nedför i backens/linjens riktning pga minustecknet?
Svar: Från envariabelanalysen är det välbekant att derivatan mäter en förändring. Tänk på samma sätt här.
Positiv derivata - tillväxt, negativ derivata - avtagande. Funktionsytan stiger som brantast då vi har det största positiva värdet på derivatan, analogt för fallet då ytan stupar som brantast.
2. Varför gör man inget med koordinaterna från städerna? Kunde man inte använda de också?
Svar: Jämför med envariabel analysen: Ändringskvoten mäter en genomsnittlig förändring. Inte samma sak som att mäta förändringen med derivata.
3. Vi gjorde ju en förenkling och räknade ut y med hjälp av de två punkterna som angavs och sedan stoppade in i formeln. Var man tvungen att göra såhär? Det går inte annars eller?
Svar: Förenklingen gjordes för att nedbringa antalet obekanta. Det underlättar kalkylen.





